题目内容
4.已知集合A={-1,0,1},B={y|y=2x-2,x∈A},则A∩B=( )| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
分析 运用列举法求出集合B,再由交集的定义,即可得到所求.
解答 解:集合A={-1,0,1},
B={y|y=2x-2,x∈A}={2-1-2,20-2,21-2}
={-$\frac{3}{2}$,-1,0},
则A∩B={-1,0},
故选:C.
点评 本题考查集合的运算,主要是交集的运算,注意运用交集的定义和列举法表示集合,属于基础题.

练习册系列答案
相关题目
14.设函数$f(x)=\sqrt{{e^x}+2x-a}$,若曲线y=cosx上存在点(x0,y0)使得f(f(y0))=y0,则实数a的取值范围是( )
| A. | [1,e] | B. | [e-1-1,1] | C. | [1,e+1] | D. | [e-1-1,e+1] |
15.设正实数x,y,则|x-y|+$\frac{1}{x}$+y2的最小值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3\root{3}{2}}{2}$ | C. | 2 | D. | $\root{3}{2}$ |
12.已知函数f(x)=alnx+x2-(a+2)x恰有两个零点,则实数a的取值范围是( )
| A. | (-1,+∞) | B. | (-2,0) | C. | (-1,0) | D. | (-2,-1) |
13.某校高二文科100名学生参加了语数英学科竞赛,年级为了解这些学生语文和数学成绩的情况,将100名学生的语文和数学成绩统计如表:
(I)若数学成绩的优秀率为35%,现利用随机抽样从数学成绩“优秀”的学生中抽取1名学生,求该生语文成绩为“及格”的概率;
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
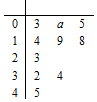 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)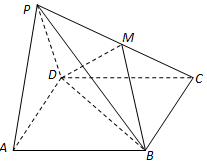 如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.