题目内容
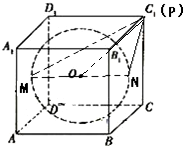
正方体ABCD-A1B1C1D1的棱长为1，MN是正方体内切球的直径，P为正方体表面上的动点，则
•
的最大值为 ．
| PM |
| PN |
考点：空间向量的数量积运算
专题：空间向量及应用
分析：连接PO，可得
•
=(
+
)•(
+
)=
2-
，当|
|取得最大值
时，即可得出
•
取得最大值．
| PM |
| PN |
| PO |
| OM |
| PO |
| ON |
| PO |
| 1 |
| 4 |
| PO |
| ||
| 2 |
| PM |
| PN |
解答：
解：连接PO，可得
•
=(
+
)•(
+
)=
2+
•(
+
)+
•
=
2-
，
当|
|取得最大值
时，
•
取得最大值为(
)2-
=
．
故答案为：
．
| PM |
| PN |
| PO |
| OM |
| PO |
| ON |
| PO |
| PO |
| OM |
| ON |
| OM |
| ON |
| PO |
| 1 |
| 4 |
当|
| PO |
| ||
| 2 |
| PM |
| PN |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了数量积运算、正方体及其内切球的性质，考查了空间想象能力，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
定义在R上的函数f（x）满足：对任意α，β∈R，总有f（α+β）-[f（α）+f（β）]=2015，则下列说法正确的是（ ）
| A、f（x）+1是奇函数 |
| B、f（x）-1是奇函数 |
| C、f（x）+2015是奇函数 |
| D、f（x）-2015是奇函数 |
复数
=（ ）
| 5 |
| 3+4i |
| A、3-4i | ||||
| B、3+4i | ||||
C、
| ||||
D、
|
摩天轮中的数学问题．如图，游乐场中的摩天轮匀速旋转，其中心O距地面40.5m，半径40m，若从最低点处登上摩天轮，那么你与地面的距离将随着时间的变化，5min后达到最高点，你登上摩天轮的时刻开始计时．请求出你与地面的距离y与时间t的函数解析式．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的函数为（ ）
| A、y=sinx |
| B、y=1g2x |
| C、y=lnx |
| D、y=-x3 |
在△ABC中，BC=1，∠B=
，△ABC的面积S=
，则AC=（ ）
| π |
| 3 |
| 3 |
| A、4 | ||
B、
| ||
C、
| ||
D、
|
函数f（x）=
sin（ωx+φ）（x∈R，ω＞0，|φ|＜
）的部分图象如图所示，则ω的值是（ ）
| 2 |
| π |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|