题目内容
9.化简tan(27°-α)•tan(49°-β)•tan(63°+α)•tan(139°-β)的结果为( )| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
分析 由条件利用诱导公式进行化简所给的式子,可得结果.
解答 解:tan(27°-α)•tan(49°-β)•tan(63°+α)•tan(139°-β)=tan(27°-α)•tan(49°-β)•cot(27°-α)•tan(41°+β)
=tan(49°-β)•tan(41°+β)=cot(41°+β)•tan(41°+β)=1,
故选:A.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
相关题目
20.以下数列是等比数列的为( )
| A. | 数列1,2,6,18,… | |
| B. | 常数列0,0,0,0,… | |
| C. | 在数列{an}中,已知$\frac{{a}_{2}}{{a}_{1}}$=2,$\frac{{a}_{3}}{{a}_{2}}$=2 | |
| D. | 在数列{an}中,$\frac{{a}_{n+1}}{{a}_{n}}$=q(其中q为非零常数,n∈N*) |
1.在等差数列{an}中,若a6+a15=10,则前20项的和S20=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 120 |
18.(-$\sqrt{x}$+$\frac{1}{x}$)10的展开式中x2的系数等于( )
| A. | 45 | B. | 20 | C. | -30 | D. | -90 |
16.如图是函数f(x)=x3+bx2+cx+d的大致图象,则b的取值范围是( )
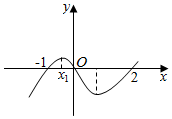

| A. | (-∞,-2) | B. | (-∞,-1) | C. | (-3,1) | D. | (1,+∞) |