题目内容
16.如图是函数f(x)=x3+bx2+cx+d的大致图象,则b的取值范围是( )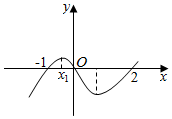
| A. | (-∞,-2) | B. | (-∞,-1) | C. | (-3,1) | D. | (1,+∞) |
分析 根据函数f(x)的大致图象,可得f′(x)=3x2+2bx+c=0有2个异号实数根,利用二次函数的性质求得b的范围.
解答 解:根据函数f(x)=x3+bx2+cx+d的大致图象,可得f′(x)=3x2+2bx+c=0有2个异号实数根,
∴$\left\{\begin{array}{l}{△={4b}^{2}-12c>0}\\{\frac{c}{3}<0}\end{array}\right.$,∴c<0 且b>3c,
结合所给的选项,
故选:A.
点评 本题主要考查三次函数的图象特征,二次函数的性质,三次函数的极值点与二次函数的零点间的关系,属于中档题.

练习册系列答案
相关题目
9.化简tan(27°-α)•tan(49°-β)•tan(63°+α)•tan(139°-β)的结果为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
4.已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且当x>2时,f(x)单调递增.如果x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)的取值范围是( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,1] | D. | (0,+∞) |
1.在△ABC中,$\overrightarrow{AB}=\overrightarrow c,\overrightarrow{BC}=\overrightarrow a,\overrightarrow{CA}=\overrightarrow b$,下列推导不正确的是( )
| A. | 若$\overrightarrow a•\overrightarrow b>0$,则△ABC为钝角三角形 | B. | $\overrightarrow a•\overrightarrow b=0$,则△ABC为直角三角形 | ||
| C. | $\overrightarrow a•\overrightarrow b=\overrightarrow b•\overrightarrow c$,则△ABC为等腰三角形 | D. | $\overrightarrow c•({\overrightarrow a+\overrightarrow b+\overrightarrow c})=0$,则△ABC为正三角形 |
5.设向量$\overrightarrow{a}$=(2sinα,1),$\overrightarrow{b}$=(1,cosα),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则锐角α为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |