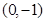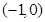题目内容
求由抛物线y2=x-1与其在点(2,1),(2,-1)处的切线所围成的面积.

【思路点拨】将抛物线方程化为y=±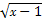 .利用导数求出其切线方程,再由定积分的几何意义求面积.
.利用导数求出其切线方程,再由定积分的几何意义求面积.
解:y=±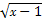 ,y'x=±
,y'x=± .
.
∵过点(2,1)的直线斜率为f'(2)= ,
,
直线方程为y-1= (x-2),即y=
(x-2),即y= x.同理,过点(2,-1)的直线方程为y=-
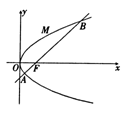
x.同理,过点(2,-1)的直线方程为y=- x,抛物线顶点在(1,0).如图所示:
x,抛物线顶点在(1,0).如图所示:
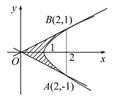
由抛物线y2=x-1与两条切线y= x,y=-
x,y=- x围成的图形面积为:
x围成的图形面积为:
S=S△AOB-2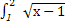 dx=
dx= ×2×2-2×
×2×2-2× ×(x-1
×(x-1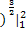 =2-
=2- (1-0)=
(1-0)= .
.
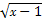 .利用导数求出其切线方程,再由定积分的几何意义求面积.
.利用导数求出其切线方程,再由定积分的几何意义求面积.解:y=±
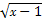 ,y'x=±
,y'x=± .
.∵过点(2,1)的直线斜率为f'(2)=
 ,
,直线方程为y-1=
 (x-2),即y=
(x-2),即y= x.同理,过点(2,-1)的直线方程为y=-
x.同理,过点(2,-1)的直线方程为y=- x,抛物线顶点在(1,0).如图所示:
x,抛物线顶点在(1,0).如图所示:
由抛物线y2=x-1与两条切线y=
 x,y=-
x,y=- x围成的图形面积为:
x围成的图形面积为:S=S△AOB-2
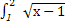 dx=
dx= ×2×2-2×
×2×2-2× ×(x-1
×(x-1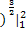 =2-
=2- (1-0)=
(1-0)= .
.
练习册系列答案
相关题目
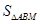 的最大值
的最大值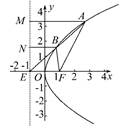
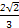
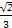


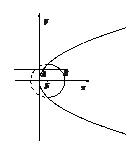
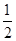 .
. ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由; 的焦点为
的焦点为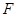 ,顶点为
,顶点为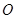 ,准线为
,准线为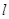 ,过该抛物线上异于顶点
,过该抛物线上异于顶点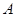 作
作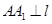 于点
于点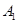 ,以线段
,以线段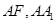 为邻边作平行四边形
为邻边作平行四边形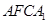 ,连接直线
,连接直线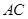 交
交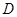 ,延长
,延长 交抛物线于另一点
交抛物线于另一点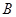 .若
.若 的面积为
的面积为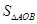 ,
,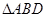 的面积为
的面积为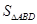 ,则
,则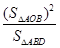 的最大值为____________.
的最大值为____________.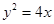 的焦点为( )
的焦点为( )