题目内容
17.已知函数f(x)=ax3-3x+2016的图象在(1,f(1))处的切线平行于x轴,则a=1.分析 求出函数的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得a=1.
解答 解:函数f(x)=ax3-3x+2016的导数为f′(x)=3ax2-3,
由图象在(1,f(1))处的切线平行于x轴,
可得f′(1)=3a-3=0,
解得a=1.
故答案为:1.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆x2+y2=($\frac{b}{2}$t+$\frac{c}{2}$)2,(c为椭圆的半焦距)对任意t∈[1,2]恒有四个不同的交点,则椭圆的离心率e的取值范围为( )
| A. | (0,$\frac{4}{5}$] | B. | ($\frac{4}{5}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | ($\frac{\sqrt{2}}{2}$,$\frac{4}{5}$) |
2.在△ABC中,点D满足$\overrightarrow{AD}$=$\frac{3}{4}\overrightarrow{AB}$,P为△ABC内一点,且满足$\overrightarrow{AP}$=$\frac{3}{10}\overrightarrow{AB}$+$\frac{2}{5}\overrightarrow{AC}$,则$\frac{{S}_{△APD}}{{S}_{△ABC}}$=( )
| A. | $\frac{3}{10}$ | B. | $\frac{9}{20}$ | C. | $\frac{6}{35}$ | D. | $\frac{9}{35}$ |
6.小冉有3条不同款式的裙子,5双不同款式的靴子,某日她要去参加聚会,若穿裙子和靴子,则不同的穿着搭配方式的种数为( )
| A. | 7 | B. | 8 | C. | 15 | D. | 125 |
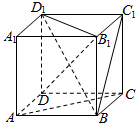 在如图所示的正方体ABCD-A1B1C1D1中:
在如图所示的正方体ABCD-A1B1C1D1中: