题目内容
17.在△ABC中,∠C=90°,M是长度为定值的BC边上一点,sin∠BAM=$\frac{1}{3}$.若$\overrightarrow{BM}•\overrightarrow{MA}$取得最大值1时,则AC的长为$\sqrt{2}$.分析 先根据向量的数量积的运算和向量的投影,以及基本不等式可得a=2,再根据正弦定理即可得到$\frac{\sqrt{{b}^{2}+1}}{3}$=$\frac{b}{\sqrt{4+{b}^{2}}}$,解得即可.
解答 解∵M是长度为定值的BC边上一点,$\overrightarrow{BM}•\overrightarrow{MA}$取得最大值为1
∴$\overrightarrow{BM}•\overrightarrow{MA}$=|$\overrightarrow{BM}$||$\overrightarrow{MA}$|cos∠AMC=|$\overrightarrow{BM}$||$\overrightarrow{MC}$|≤1,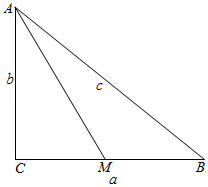
∴当且仅当|$\overrightarrow{BM}$|=|$\overrightarrow{MC}$|=1时取等号,
∴a=2,
设AC=b,AB=c,CM=MB=$\frac{1}{2}$a=1,
在△ABM中,由正弦定理可得,$\frac{BM}{sin∠BAM}$=$\frac{AM}{sinB}$,即$\frac{\sqrt{{b}^{2}+1}}{sinB}$=$\frac{1}{\frac{1}{3}}$=3,
∴sinB=$\frac{\sqrt{{b}^{2}+1}}{3}$,
在△ABC中,sinB=$\frac{b}{c}$=$\frac{b}{\sqrt{4+{b}^{2}}}$,
∴$\frac{\sqrt{{b}^{2}+1}}{3}$=$\frac{b}{\sqrt{4+{b}^{2}}}$,
解得b=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查正弦定理的应用向量的数量的积,向量的投影,基本不等式成立的条件,以及勾股定理的应用,属中档题.

 名师点拨卷系列答案
名师点拨卷系列答案| A. | {x|x<-2或x>3} | B. | {x|x<-3或x>2} | C. | {x|-2<x<3} | D. | {x|-3<x<2} |
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{BA}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AC}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$ |
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
| A. | 1 | B. | $\frac{8}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{10}{7}$ |