题目内容
抛物线y2=12x的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,当△FPM为等边三角形时,则△FPM的外接圆的方程为 .
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:利用抛物线的定义得出PM垂直于抛物线的准线,设M(-3,m),则P(9,m),求出△PMF的边长,写出有关点的坐标,得到外心Q的坐标,△FPM的外接圆的半径,从而求出其方程.
解答:
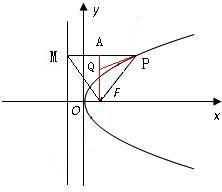 解:据题意知,△PMF为等边三角形,PF=PM,
解:据题意知,△PMF为等边三角形,PF=PM,
∴PM⊥抛物线的准线,F(3,0)
设M(-3,m),则P(9,m),等边三角形边长为12,如图.
在直角三角形APF中,PF=12,解得外心Q的坐标为(3,±4
). 则△FPM的外接圆的半径为4
,
∴则△FPM的外接圆的方程为(x-3)2+(y±4
)2=48.
故答案为:(x-3)2+(y±4
)2=48.
 解:据题意知,△PMF为等边三角形,PF=PM,
解:据题意知,△PMF为等边三角形,PF=PM,∴PM⊥抛物线的准线,F(3,0)
设M(-3,m),则P(9,m),等边三角形边长为12,如图.
在直角三角形APF中,PF=12,解得外心Q的坐标为(3,±4
| 3 |
| 3 |
∴则△FPM的外接圆的方程为(x-3)2+(y±4
| 3 |
故答案为:(x-3)2+(y±4
| 3 |
点评:本题主要考查了抛物线的简单性质,直线与抛物线的综合问题.考查了学生综合把握所学知识和基本的运算能力

练习册系列答案
相关题目
 如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设
如图,已知△ABC中,点D在边BC上,且|BD|=2|DC|,点E在线段AD上,且|AE|=2|ED|,设 如图,在平面直角坐标系xoy中,椭圆E:
如图,在平面直角坐标系xoy中,椭圆E: 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=PB=PC,PO⊥AD,O为BC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=PB=PC,PO⊥AD,O为BC的中点.