题目内容
一个直角三角形的三边长分别为3cm、4cm、5cm，则它绕斜边旋转一周形成的几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：几何体的体积是由上下两个圆锥的体积组成的，它们的底面半径相同，都是直角三角形斜边上的高，利用圆锥体积公式，即可求得结论．．
解答：
解：如图，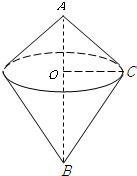
斜边的高为：3×4÷5=
（厘米），
以AC为母线的圆锥体积=
π•(
)2•AO，
以BC为母线的圆锥体积=
π•(
)2•BO，
∴绕斜边旋转一周形成的几何体的体积等于
π•(
)2•AB=
πcm3．
故选：B．
斜边的高为：3×4÷5=| 12 |
| 5 |
以AC为母线的圆锥体积=
| 1 |
| 3 |
| 12 |
| 5 |
以BC为母线的圆锥体积=
| 1 |
| 3 |
| 12 |
| 5 |
∴绕斜边旋转一周形成的几何体的体积等于
| 1 |
| 3 |
| 12 |
| 5 |
| 48 |
| 5 |
故选：B．
点评：本小题主要考查圆锥的体积公式以及几何旋转体的知识等基础知识，考查运算求解能力，考查空间想象力．得到这个立体图形是由两个圆锥组成，以及圆锥体积公式求出是解决问题的关键．
练习册系列答案
相关题目
若
=k，则
等于（ ）
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| lim |
| △x→0 |
| f(x0+2•△x)-f(x0) |
| △x |
| A、2k | ||
| B、k | ||
C、
| ||
| D、以上都不是 |
将函数y=2sinxsin（
+x）的图象向右平移φ（φ＞0）个单位长度，使平移后的图象仍过点（
，
），则φ的最小值为（ ）
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}的前n项和Sn和通项an满足Sn=
（1-an），则数列{an}的通项公式为（ ）
| 1 |
| 2 |
A、an=（
| ||
B、an=（
| ||
C、an=（
| ||
D、an=3•（
|
若a＞b，c∈R，则下列关系一定成立的是（ ）
| A、ac2＞bc2 | ||||
| B、ac＞bc | ||||
| C、a+c＞b+c | ||||
D、
|
“x=2kπ+
（k∈z）”是“sinx=
”成立的（ ）
| π |
| 4 |
| ||
| 2 |
| A、充分不必要条件 |
| B、必要不充分条 |
| C、充分条件 |
| D、既不充分也不必要条件 |
已知p：|x|＜2；q：x2-x-2＜0，则q是p的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |