题目内容
已知直线l、m、n与平面α、β,给出下列四个命题( )
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α或m?α.
其中假命题是( )
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α或m?α.
其中假命题是( )
| A、① | B、② | C、③ | D、④ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:由公理4,即可判断①;可线面平行的性质定理和面面垂直的判定定理,即可判断②;
由线面平行的性质和线线位置关系,即可判断③;由线面垂直和面面垂直的性质,结合线面位置关系,即可判断④.
由线面平行的性质和线线位置关系,即可判断③;由线面垂直和面面垂直的性质,结合线面位置关系,即可判断④.
解答:
解:①若m∥l,n∥l,则m∥n,由公理4知,①对;
②若m⊥α,m∥β,过m的平面为γ,令γ∩β=l,则m∥l,即有l⊥α,l?β,α⊥β,故②对;
③若m∥α,n∥α,则m,n平行、相交或异面,故③错;
④若m⊥β,α⊥β,则在α内作一条直线l垂直于α,β的交线,则l⊥β,m∥l,故有m∥α,
或m?α,m⊥β.故④对.
故选C.
②若m⊥α,m∥β,过m的平面为γ,令γ∩β=l,则m∥l,即有l⊥α,l?β,α⊥β,故②对;
③若m∥α,n∥α,则m,n平行、相交或异面,故③错;
④若m⊥β,α⊥β,则在α内作一条直线l垂直于α,β的交线,则l⊥β,m∥l,故有m∥α,
或m?α,m⊥β.故④对.
故选C.
点评:本题考查空间线线的位置关系,线面位置关系,主要是平行或垂直,考查面面垂直的判定和性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):则( )
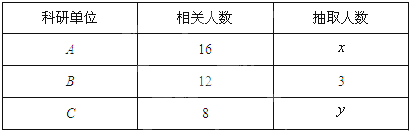

| A、x=6,y=4 |
| B、x=4,y=3 |
| C、x=7,y=4 |
| D、x=4,y=2 |
f(x)=3x+5,g(x)=log3(x3-5),则y=f(g(x))是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
若直线x=k与曲线y=log2x及y=log2(x+2)分别相交,且交点之间的距离大于1,则k的取值范围是( )
| A、(0,1) |
| B、(0,2) |
| C、(1,2) |
| D、(2,+∞) |
有50件产品,编号为0,1,2,…,49,现从中抽取5个进行检验,用系统抽样的方法抽取样本的编号可以为( )
| A、5,10,15,20,25 |
| B、5,13,21,29,37 |
| C、8,22,23,1,20 |
| D、1,11,21,31,41 |
若某组合体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、10 | ||
| D、12 |