题目内容
12.已知O是△ABC外接圆的圆心,已知△ABC外接圆半径为2,若$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$,则边长AB=3.分析 由$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$,得16R2+25R2+40R2cos∠AOB=36R2,即8cos∠AOB=-1,
由2∠ACB=∠AOB,得cosC=$\frac{\sqrt{7}}{4}$⇒sin∠ACB=$\frac{3}{4}$
由$\frac{AB}{sin∠ACB}=2R=4$⇒AB=4sin∠ACB=3
解答 解:设△ABC的外接圆的半径为R,因为$4\overrightarrow{OA}+5\overrightarrow{OB}+6\overrightarrow{OC}=\vec 0$,
所以$4\overrightarrow{OA}+5\overrightarrow{OB}=-6\overrightarrow{OC}$,则16R2+25R2+40R2cos∠AOB=36R2,即8cos∠AOB=-1,
解得:cos∠AOB=-$\frac{1}{8}$.
由2∠ACB=∠AOB,
2cos2∠ACB-1=cos∠AOB=-$\frac{1}{8}$,则cosC=$\frac{\sqrt{7}}{4}$⇒sin∠ACB=$\frac{3}{4}$
由$\frac{AB}{sin∠ACB}=2R=4$⇒AB=4sin∠ACB=3
故答案为:3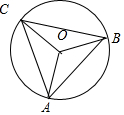
点评 本题考查向量的运算和三角形外心的性质和应用,二倍角公式,解题时要认真审题,仔细解答,注意向量运算法则的灵活运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数y=2x+3在区间[1,5]上的最大值是( )
| A. | 5 | B. | 10 | C. | 13 | D. | 16 |
3.下列函数中,满足“对任意x1,x2∈(0,+∞),x1≠x2,均有$\frac{f{(x}_{1})-f{(x}_{2})}{{x}_{1}{-x}_{2}}$>0”的是( )
| A. | f(x)=2lg(x-1) | B. | f(x)=(x+1)2 | C. | f(x)=e-x | D. | f(x)=$\frac{1}{x}$ |
7.下列对于函数f(x)=3+cos2x,x∈(0,3π)的判断正确的是( )
| A. | 函数f(x)的周期为π | |
| B. | 对于?a∈R,函数f(x+a)都不可能为偶函数 | |
| C. | ?x0∈(0,3π),使f(x0)>4 | |
| D. | 函数f(x)在区间$[\frac{π}{2},\frac{5π}{4}]$内单调递增 |
1.已知不等式ln(x+1)-1≤ax+b对一切x>-1都成立,则$\frac{b}{a}$的最小值是( )
| A. | e-1 | B. | e | C. | 1-e-3 | D. | 1 |
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于$\frac{\sqrt{3}}{3}$.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于$\frac{\sqrt{3}}{3}$.