题目内容
10.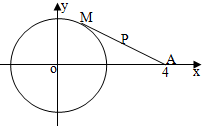 已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,
已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,(1)求点P的轨迹C的方程
(2)过点A的直线与轨迹C有公共点,求的斜率k的取值范围.
分析 (1)设AM中点P(x,y),则M(2x-4,2y),代入圆的方程得点P的轨迹C的方程;
(2)过点A的直线与轨迹C有公共点,圆心(2,0)到直线的距离d=$\frac{|-2k|}{\sqrt{{k}^{2}+1}}$≤1,即可求斜率k的取值范围.
解答 解:(1)设AM中点P(x,y),则M(2x-4,2y),
代入圆的方程得(2x-4)2+4y2=4,即(x-2)2+y2=1.
(2)设过点A的直线方程为y=k(x-4),即kx-y-4k=0,
∵过点A的直线与轨迹C有公共点,
∴圆心(2,0)到直线的距离d=$\frac{|-2k|}{\sqrt{{k}^{2}+1}}$≤1,
∴-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$.
点评 本题考查代入法求轨迹方程,考查直线与圆的位置关系,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
18.已知x1,x2(x1<x2)是函数f(x)=lnx-$\frac{1}{x-1}$的两个零点,若a∈(x1,1),b∈(1,x2),则( )
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |
19.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共80人,患胃病者生活规律的共20人,未患胃病者生活不规律的共240人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| ko | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
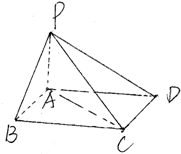 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD