题目内容
19.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共80人,患胃病者生活规律的共20人,未患胃病者生活不规律的共240人,未患胃病者生活规律的共200人.(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| ko | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)由已知能列出2×2列联表.
(2)根据列联表中的数据,得$\begin{array}{l}{K^2}=\frac{{540(20×240-80×200{)^2}}}{220×320×100×440}≈21.868>10.828\end{array}$,从而得到在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病与否和生活规律有关.
解答 解:(1)由已知可列2×2列联表:
| 患胃病 | 未患胃病 | 总计 | |
| 生活规律 | 20 | 200 | 220 |
| 生活不规律 | 80 | 240 | 320 |
| 总计 | 100 | 440 | 540 |
因此,在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病与否和生活规律有关.
点评 本题考查2×2列联表的列法和独立性检验的应用,是中档题,解题时要认真审题,注意K2的计算公式的合理运用.

练习册系列答案
相关题目
9.已知长方体ABCD-A1B1C1D1,AB=BC=2,CC1=2$\sqrt{2}$,E为CC1的中点,则点A到平面BED的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2、 |
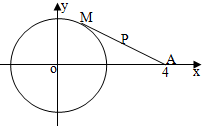 已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,
已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,点E是PC的中点,F在直线PA上.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,点E是PC的中点,F在直线PA上.