题目内容

18．已知x1，x2（x1＜x2）是函数f（x）=lnx-$\frac{1}{x-1}$的两个零点，若a∈（x1，1），b∈（1，x2），则（　　）
A．f（a）＜0，f（b）＜0B．f（a）＞0，f（b）＞0C．f（a）＞0，f（b）＜0D．f（a）＜0，f（b）＞0

分析 令函数f（x）=lnx-$\frac{1}{x-1}$=0，利用图象求出零点的位置，数形结合法，可得答案．

解答 解：已知x1，x2（x1＜x2）是函数f（x）=lnx-$\frac{1}{x-1}$的两个零点，
令函数f（x）=lnx-$\frac{1}{x-1}$=0，可得lnx=$\frac{1}{x-1}$，
则函数y=lnx与y=$\frac{1}{x-1}$的图象如下
当a∈（x1，1）时，
则lna＞$\frac{1}{a-1}$，
∴则f（a）=lna-$\frac{1}{a-1}$＞0，
同理：当b∈（1，x2），
则lnb＜$\frac{1}{b-1}$，
∴则f（b）=lna-$\frac{1}{b-1}$＜0，
故选C．

点评 本题考查函数图象的画法零点的问题的转化，利用了数形结合法．属于中档题．

练习册系列答案
相关题目
8．已知曲线C的参数方程为$\left\{\begin{array}{l}x=-2+\sqrt{10}cosα\\ y=\sqrt{10}sinα\end{array}\right.$（α为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为$ρcos（{θ-\frac{π}{4}}）=2\sqrt{2}$
（1）求曲线C的普通方程和直线l的直角坐标方程；
（2）设点P是曲线C上的一个动点，求它到直线l的距离d的取值范围．
9．已知长方体ABCD-A1B1C1D1，AB=BC=2，CC1=2$\sqrt{2}$，E为CC1的中点，则点A到平面BED的距离为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2、
6．已知A（x1，y1），B（x2，y2）是抛物线y2=x上相异的两点，且在x轴同侧，点C（1，0）．若直线AC，BC的斜率互为相反数，则y1y2等于（　　）
A．1B．2C．3D．4
13．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为f（x）的上界．已知函数$f（x）=1+a{（\frac{b}{2}）^x}+{（\frac{c}{4}）^x}$．
（Ⅰ）当a=b=c=1时，求函数f（x）在（-∞，0）上的值域，并判断函数f（x）在（-∞，0）上是否有上界，请说明理由；
（Ⅱ）若b=c=1，函数f（x）在[0，+∞）是以3为上界的有界函数，求实数a的取值范围．
（Ⅲ）已知s为正整数，当a=1，b=-1，c=0时，是否存在整数λ，使得对任意的n∈N•，不等式s≤λf（n）≤s+2恒成立？若存在，求出λ的值；若不存在，说明理由．
3．如图，已知正四棱柱ABCD-A1B1C1D1的底面边长是2，侧棱长是16，M，N分别是棱BB1、B1C1的中点．
（1）求异面直线MN与A1C1所成角的大小（结果用反三角表示）
（2）求直线MN与平面ACC1A1所成的角（结果用反三角函数表示）]．
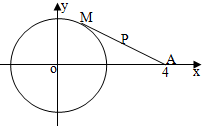10．已知点M是⊙O：x2+y2=4上一动点，A（4，0），点P为线段AM的中点，
（1）求点P的轨迹C的方程
（2）过点A的直线与轨迹C有公共点，求的斜率k的取值范围．
7．已知函数f（x）=（sinx+cos）2+2$\sqrt{3}$sin2x
（1）求函数f（x）的最小正周期并求出单调递增区间；
（2）在△ABC中，角A，B，C的对边分别是a，b，c，且满足2acosC+c=2b，求f（B）的取值范围．
8．已知函数f（x）=x2+ax+b（a，b∈R），如果?x0，使f（x0）=0．且?x∈R，都有f（x）≥f（x0）成立．又若关于x的不等式f（x）＜c的解集为（m，m+8），则实数c的值为16．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网