题目内容
20.函数f(x)=xe-x,x∈[0,4]的最小值是0.分析 先求出导函数f′(x),由f′(x)>0和f′(x)<0,求出x的取值范围,得出函数f(x)的单调区间,从而求出函数的最值.
解答 解:函数f(x)=xe-x,可得f′(x)=$\frac{1-x}{{e}^{x}}$,
当x∈[0,1)时,f′(x)>0,f(x)单调递增,当x∈(1,4]时,f′(x)<0,f(x)单调递减,
∵f(0)=0,f(4)=$\frac{4}{{e}^{4}}$>0,∴当x=0时,f(x)有最小值,且f(0)=0.
故答案为:0.
点评 本题考查的是利用导数,判断函数的单调性,从而求出最值,属于基础题.

练习册系列答案
相关题目
13.设f(x)=xa-ax(0<a<1),则f(x)在[0,+∞)内的极大值点x0等于( )
| A. | 0 | B. | a | C. | 1 | D. | 1-a |
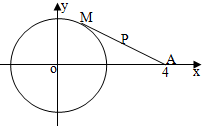 已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,
已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点, 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,点E是PC的中点,F在直线PA上.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,点E是PC的中点,F在直线PA上.