题目内容

4．已知$sin（{65°+α}）=\frac{1}{3}$，则cos（25°-α）的值为（　　）
A．$-\frac{1}{3}$B．$\frac{1}{3}$C．$-\frac{{2\sqrt{2}}}{3}$D．$\frac{{2\sqrt{2}}}{3}$

分析 由已知利用诱导公式即可计算求值．

解答 解：∵$sin（{65°+α}）=\frac{1}{3}$，
∴cos（25°-α）=cos[90°-（65°+α）]=$sin（{65°+α}）=\frac{1}{3}$．
故选：B．

点评 本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题．

练习册系列答案
相关题目
16．已知△ABC的内角A，B，C所对的边分别为a，b，c，若向量$\overrightarrow{m}$=（a，b+c），$\overrightarrow{n}$=（cosC+$\sqrt{3}$sinC，-1）相互垂直．
（1）求角A的大小；
（2）若a=$\sqrt{3}$，求△ABC周长的最大值．
15．对于函数f（x），g（x）满足：对任意x∈R，都有f（x2-2x+3）=g（x），若关于x的方程g（x）+sin$\frac{π}{2}$x=0只有5个根，则这5个根之和为（　　）
A．5B．6C．8D．9
12．已知f（x）是定义在R上的奇函数，当x＜0时，f（x）=ex（x+1），给出以下命题：
①当x＞0时，f（x）=ex（1-x）；
②f（x）有3个零点；
③f（x）＞0的解集为（-1，0）∪（1，+∞）；
④?x1，x2∈R，都有|f（x1）-f（x2）|≤2，
其中正确命题的序号是②③④（填上所有正确命题的序号）
19．若函数f（x）=-$\frac{a}{b}$lnx-$\frac{a+1}{b}$（a＞0，b＞0）的图象在x=1处的切线与圆x2+y2=1相切，则a+b的最大值是（　　）
A．4B．2$\sqrt{2}$C．2D．$\sqrt{2}$
9．已知集合$A=\{x|y=\sqrt{2-x}\}$，B={x|x2-2x＜0}，则A∩B=（　　）
A．（0，2]B．（0，2）C．（-∞，2]D．（2，+∞）
16．有三对师徒共6个人，站成一排照相，每对师徒相邻的站法共有（　　）
A．72B．54C．48D．8
13．一几何体的三视图是如图所示的三个直角边为2的等腰直角三角形，则该几何体的表面积为（　　）
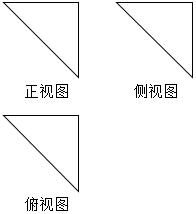
A．8B．4$\sqrt{3}$+4C．4$\sqrt{2}$+4D．6+2$\sqrt{3}$
14．设a∈R，则“a＞1”是“a2＞|a-2|”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网