题目内容
5.已知数列{an}的各项均为正数,Sn为其前n项和,对于任意的n∈N*,Sn=2an-2.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的前n项和为Tn,且bn=$\frac{1}{(lo{g}_{2}{a}_{n})^{2}}$,求证:对任意正整数n,总有Tn<2.
分析 (I)对于任意的n∈N*,Sn=2an-2,当n=1时,a1=2a1-2,解得a1=2;当n≥2时,$\frac{{a}_{n}}{{a}_{n-1}}$=2,利用等比数列的通项公式即可得出;
(II)bn=$\frac{1}{(lo{g}_{2}{a}_{n})^{2}}$=$\frac{1}{{n}^{2}}$,当n≥2时,$\frac{1}{{n}^{2}}$≤$\frac{1}{n(n+1)}$,利用“裂项求和”即可证明.
解答 (I)解:∵对于任意的n∈N*,Sn=2an-2,
∴当n=1时,a1=2a1-2,解得a1=2;
当n≥2时,Sn-1=2an-1-2,
∴an=2an-2an-1,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=2,
∴数列{an}是等比数列,首项为2,公比为2,
∴${a}_{n}={2}^{n}$.
(II)bn=$\frac{1}{(lo{g}_{2}{a}_{n})^{2}}$=$\frac{1}{{n}^{2}}$,
∴Tn=$1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$≤1+$\frac{1}{1×2}+\frac{1}{2×3}$+…+$\frac{1}{n(n+1)}$=1+$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=2-$\frac{1}{n}$<2.
点评 本题考查了数列的递推式、等比数列的通项公式、“裂项求和”与“放缩法”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知点P为曲线xy-$\frac{5}{2}$x-2y+3=0上任意一点,O为坐标原点,则|OP|的最小值为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
17.定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(x+1)在(0,+∞)上恰有三个零点,则a的取值范围是( )
| A. | (0,$\frac{{\sqrt{2}}}{2}$) | B. | (0,$\frac{{\sqrt{3}}}{3}$) | C. | (0,$\frac{{\sqrt{5}}}{5}$) | D. | ($\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{3}}}{3}$) |
13. 某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
 某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )
某中学为了检验1000名在校高三学生对函数模块掌握的情况,进行了一次测试,并把成绩进行统计,得到的样本频率分布直方图如图所示,则考试成绩的中位数大约(保留两位有效数字)为( )| A. | 70 | B. | 73 | C. | 75 | D. | 76 |
20.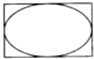 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A. | 17.84 | B. | 18.84 | C. | 5.16 | D. | 6.16 |
13.把复数z的共轭复数记作$\overline{z}$,复数z=3-i(i为虚数单位),则复数$\frac{\overline{z}}{1+i}$在复平面内所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.已知i是虚数单位,则|$\frac{1-i}{1+i}$|=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |