题目内容
14.已知i是虚数单位,则|$\frac{1-i}{1+i}$|=( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用复数代数形式的乘除运算化简,然后利用复数模的公式求模.
解答 解:|$\frac{1-i}{1+i}$|=$|\frac{(1-i)^{2}}{(1+i)(1-i)}|=|\frac{-2i}{2}|=|-i|=1$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
2.将$y=sin(x+\frac{π}{3})$的图象上各点的横坐标缩短到原来的一半,纵坐标不变,再将图象上所有点向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴为( )
| A. | $x=-\frac{π}{12}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{π}{2}$ |
6.已知z=$\frac{2+i}{1-2i}$,则|z|+z=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
 和点
和点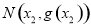 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且 ,若直线
,若直线 轴,则
轴,则 两点间的距离的最小值为( )
两点间的距离的最小值为( ) ,设
,设 ,且
,且 ,则
,则 的最小值为( )
的最小值为( ) D.
D.