题目内容
已知x、y满足条件
,若目标函数z=ax+y(a∈R)取得最大值时的最优解有无数个,则z=ax+y的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z=ax+y取得最大值的最优解有无穷多个,得到目标函数的对应的直线和不等式对应的边界的直线的斜率相同,解方程即可得到结论.
解答:
解:不等式对应的平面区域如图:
由z=ax+y得y=-ax+z,
若a=0时,直线y=-ax+z=z,此时取得最大值的最优解只有一个,不满足条件.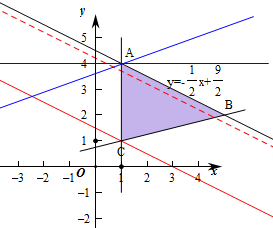
若-a>0,则直线y=-ax+z截距取得最大值时,z取的最大值,此时直线只在A处取得最大值,最优解只有一个,不满足条件,
若-a<0,则直线y=-ax+z截距取得最大值时,z取的最大值,此时满足直线y=-ax+z与AB平行,
直线AB为y=-
x+
,直线的斜率k=-
,
此时-a=-
,解得a=
.
综上满足条件的a=-
,即目标函数为y=-
x+z,
当直线y=-
x+z经过点C时,直线的截距最小,此时z有最小值,
由
,解得
,即A(1,1),
此时z=
+1=
,
故选:B.
由z=ax+y得y=-ax+z,
若a=0时,直线y=-ax+z=z,此时取得最大值的最优解只有一个,不满足条件.

若-a>0,则直线y=-ax+z截距取得最大值时,z取的最大值,此时直线只在A处取得最大值,最优解只有一个,不满足条件,
若-a<0,则直线y=-ax+z截距取得最大值时,z取的最大值,此时满足直线y=-ax+z与AB平行,
直线AB为y=-
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
此时-a=-
| 1 |
| 2 |
| 1 |
| 2 |
综上满足条件的a=-
| 1 |
| 2 |
| 1 |
| 2 |
当直线y=-
| 1 |
| 2 |
由
|
|
此时z=
| 1 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题主要考查线性规划的应用,利用z的几何意义,结合z=ax+y取得最大值的最优解有无穷多个,利用结合数形结合先求出a是解决本题的根据.

练习册系列答案
相关题目
下列命题中,正确的个数为( )
①“a+5是无理数”是“a是无理数”的充要条件;
②“x<5”是“x<3”的充分不必要条件;
③过点P(2,3)且在两轴上的截距相等的直线方程是x+y-5=0.
①“a+5是无理数”是“a是无理数”的充要条件;
②“x<5”是“x<3”的充分不必要条件;
③过点P(2,3)且在两轴上的截距相等的直线方程是x+y-5=0.
| A、0 | B、1 | C、2 | D、3 |
双曲线
-
=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、2
|
设双曲线
-
=1(a>0,b>0)的实轴长为6,F(5,0)是双曲线的一个焦点,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
若
=
,
=
,则∠AOB平分线上的向量
为( )
| OA |
| a |
| OB |
| b |
| OM |
A、
| ||||||||||||||||
B、λ(
| ||||||||||||||||
C、
| ||||||||||||||||
D、λ(
|
复数
=( )
| (1+i)2 |
| i2 |
| A、2i | B、-2i | C、2 | D、-2 |
下列各选项中,与sin2008°最接近的数是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设函数f(x)、g(x)分别是定义在R上的奇函数和偶函数,f′(x),g′(x)分别是f(x),g(x)的导函数,当x<0时,f′(x)•g(x)+f(x)•g′(x)>0且g(-3)=0,则f(x)•g(x)<0的解集是( )
| A、(-3,0)∪(0,3) |
| B、(-3,0)∪(3,+∞) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |