题目内容
【题目】已知数列{an}共有2k项(![]() ),数列{an}的前n项和为Sn,满足:a1 = 2,an1 = (p 1) Sn 2(n = 1,2,…, 2k1),其中常数p > 1.
),数列{an}的前n项和为Sn,满足:a1 = 2,an1 = (p 1) Sn 2(n = 1,2,…, 2k1),其中常数p > 1.
(1)求证:数列{an}是等比数列;
(2)若![]() ,数列{bn }满足
,数列{bn }满足![]() (n = 1,2,…, 2k),求数列
(n = 1,2,…, 2k),求数列
{bn }的通项公式;
(3)对于(2)中数列{bn },求和Tn = ![]() .
.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)先根据关系![]() 得递推关系式:
得递推关系式: ![]() ,再根据等比数列定义得证(2)先根据等比数列通项公式得an = a1p n 1.代入条件,利用指数性质化简得
,再根据等比数列定义得证(2)先根据等比数列通项公式得an = a1p n 1.代入条件,利用指数性质化简得 ![]() .(3)关键取绝对值,因为
.(3)关键取绝对值,因为![]() ,所以当n≤k时,
,所以当n≤k时, ![]() ;当n≥k1时,
;当n≥k1时, ![]() .再分别按等差数列求和得结果.
.再分别按等差数列求和得结果.
试题解析:解:(1)∵an1 = (p 1)Sn 2(n = 1,2,…, 2k1),
∴an = (p 1)Sn 1 2(n = 2,…, 2k).
则当n = 2,…, 2k1时,两式相减,得
an1 an = (p 1)(Sn Sn 1),即an1 an = (p 1) an.
∴an1 = pan(n = 2,…, 2k1).
原式中,令n = 1,得a2 = (p 1)a1 2 = 2 (p 1) 2 = 2p = pa1.
∴an1 = pan,即![]() (n = 1,2,…, 2k1).
(n = 1,2,…, 2k1).
则数列{an}是等比数列.
(2)由(1),得an = a1p n 1.
∴![]()
![]()
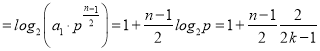
![]() .
.
(3)∵![]() ,
,
∴当n≤k时, ![]() ;当n≥k1时,
;当n≥k1时, ![]() .
.
则![]()
=![]()
=![]() =
=![]()
=![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目