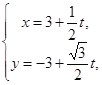题目内容
【题目】![]() 的内角
的内角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() .
.
【答案】(1)A=![]() ;(2)b=c=1.
;(2)b=c=1.
【解析】
试题分析:(1)结合已知条件并运用正弦定理即可得出![]() ,再由三角形内角和为π即可得出角
,再由三角形内角和为π即可得出角![]() 的大小即可;(2)由三角形的面积公式S=
的大小即可;(2)由三角形的面积公式S=![]() bcsinA即可求出bc的值,然后结合(1)并运用余弦定理即可得出关于b,c的另一个等式关系,再联立方程组即可求出b,c的值即可.
bcsinA即可求出bc的值,然后结合(1)并运用余弦定理即可得出关于b,c的另一个等式关系,再联立方程组即可求出b,c的值即可.
试题解析:(1)由已知结合正弦定理可得sinC=![]() sinAsinC﹣sinCcosA,∵sinC≠0,
sinAsinC﹣sinCcosA,∵sinC≠0,
∴1=![]() sinA﹣cosA=2sin(A﹣
sinA﹣cosA=2sin(A﹣![]() ),即sin(A﹣
),即sin(A﹣![]() )=
)=![]() , 又∵A∈(0,π),∴A﹣
, 又∵A∈(0,π),∴A﹣![]() ∈(﹣
∈(﹣![]() ,
,![]() ),∴A﹣
),∴A﹣![]() =
=![]() ,∴A=
,∴A=![]() .
.
(2)S=![]() bcsinA,即
bcsinA,即![]() =
=![]() bc
bc![]() ,∴bc=1,①
,∴bc=1,①
又∵a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccos![]() ,即1=(b+c)2﹣3,且b,c为正数,∴b+c=2,②
,即1=(b+c)2﹣3,且b,c为正数,∴b+c=2,②
由①②两式解得b=c=1.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
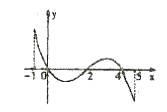
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.
【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: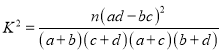 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |