题目内容
【题目】如图，三棱锥P-ABC中，PA
平面ABC，
（1）（Ⅰ）求三棱锥P-ABC的体积；
（2）（Ⅱ）证明：在线段PC上存在点M，使得ACBM，并求
的值.
【答案】
（1）
（2）
【解析】（I）由题设AB=1，AC=2，
，可得
.由PA
平面ABC,可知PA是三棱锥P-ABC的高，体积
.
（II）证：在平面ABC内，过点B作BNAC,垂足为N，过N作MN//PA交PC于M,连接BM，由PA面ABC知PAAC,所以MNAC,由于BN
MN=N,故AC面MBN,又BM
面MBN,所以ACBM.
在直角
BAN中，AN=AB
,从而NC=AC-AN=
，由MN//PA,得
.
【考点精析】认真审题，首先需要了解向量语言表述线面的垂直、平行关系(要证明一条直线和一个平面平行，也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线
的方向向量是
，平面
内的两个相交向量分别为
，若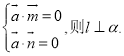
)．
练习册系列答案
相关题目
【题目】
全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标．根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据，对名列前20名的“省级卫视新闻台”的融合指数进行分组统计，结果如表所示．求：（1）现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在[7,8]的概率；（2）根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数．
组号 | 分组 | 频数 |
1 | [4,5） | 2 |
2 | [5,6） | 8 |
3 | [6,7） | 7 |
4 | [7,8] | 3 |
（1）现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在[7,8]的概率；
（2）根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数．
