Question

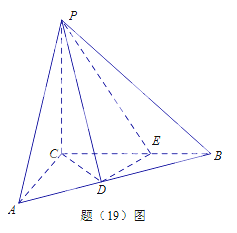
【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC，VAB为等比三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。
（I）求证：VB//平面MOC；
（II）求证：平面MOC平面VAB；
（III）求三棱锥V-ABC的体积。

Answer 1

【答案】（I）证明详见解析；（II）证明详见解析；（III）
【解析】
（I）因为O,M分别为AB,VA的中点，
所以OM//VB
又因为VB平面MOC
所以VB//平面MOC
（II）因为AC=BC,O为AB的中点，
所以OCAB
又因为平面VAB平面ABC，且OC平面ABC，
所以OC平面VAB。
（III）在等腰直角三角形ACB中，AC=BC=，
所以AB=2，OC=1.
所以等边三角形VAB的面积.
又因为CO平面VAB,
所以三棱锥C-VAB的体积等于.
又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等，
所以三棱锥V-ABC的体积为。
【考点精析】通过灵活运用向量语言表述线面的垂直、平行关系，掌握要证明一条直线和一个平面平行，也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线的方向向量是，平面内的两个相交向量分别为，若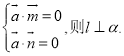即可以解答此题．