题目内容
已知定义在R上的函数f(x)和数列{an}满足下列条件:
a1=a,an=f(aa-1)(n=2,3,4,…),a2≠a1,f(an)-f(an-1)=k(an-an-1)(n=2,3,4,…),其中a为常数,k为非零常
数.
(Ⅰ)令bn=aa+1-an(n∈N*),证明数列{bn}是等比数列;
(Ⅱ)求数列{an}的通项公式 ;
;
(Ⅲ)当|k|<1时,求
易错起源4、数列与解析几何、函数、不等式的综合
【错误答案】(Ⅰ)证明:由b1=a2-a1≠0,可得:b2=a3-a2=f(a2)-f(a1)=k(a2-a1)≠0.由数学归纳法可证bn=an+1-an≠0(n∈N*).由题设条件,当n≥2时
 =k
=k
故数列{bn}是公比为k的等比数列.


练习册系列答案
相关题目
 ,x∈R},B={x∣
,x∈R},B={x∣ }。若
}。若 ,求实数a的取值范围。
,求实数a的取值范围。 ,则下列正确的是 ( )
,则下列正确的是 ( ) (an-1)(n∈N*).
(an-1)(n∈N*). Ⅰ) 求a1,a2;
Ⅰ) 求a1,a2;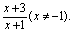 设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-
设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an-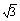 |,Sn=b1+b2+…+bn(n∈N*).
|,Sn=b1+b2+…+bn(n∈N*).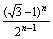 ;
;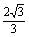 .
. ,用Ⅱn
,用Ⅱn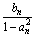 ,又知P0(
,又知P0(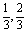 ).
).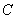 在
在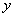 轴右侧,
轴右侧, 的距离减去它到
的距离减去它到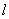 交曲线
交曲线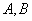 两点,线段
两点,线段 的中点为
的中点为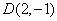 ,求直线
,求直线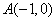 ,
,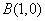 ,
,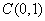 ,直线
,直线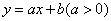 将
将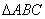 分割为面积相等的两部分,则
分割为面积相等的两部分,则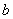 的取值范围是( )
的取值范围是( ) (B)
(B)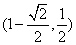 (C)
(C)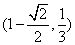 (D)
(D)