题目内容
若函数f(x)=ax-a-x存在唯一的零点x0,则当x0>x>0时,恒有( )
| A、f(x)<0 |
| B、1-a>f(x)>0 |
| C、f(x)>1-a |
| D、以上判断都有可能 |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:根据条件确定a的取值范围,利用函数的单调性即可得到结论.
解答:
解:由f(x)=ax-a-x=0得ax=x+a,
若a>1,函数y=ax与y=x+a有两个交点,不满足条件,
若0<a<1,函数y=ax与y=x+a有1个交点,不足条件,
即若函数f(x)=ax-a-x存在唯一的零点x0,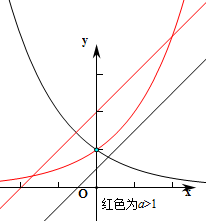
则0<a<1,此时函数f(x)=ax-a-x单调递减,
若x0>x>0,则f(x0)<f(x)<f(0),
即0<f(x)<1-a,
故选:B
若a>1,函数y=ax与y=x+a有两个交点,不满足条件,
若0<a<1,函数y=ax与y=x+a有1个交点,不足条件,
即若函数f(x)=ax-a-x存在唯一的零点x0,

则0<a<1,此时函数f(x)=ax-a-x单调递减,
若x0>x>0,则f(x0)<f(x)<f(0),
即0<f(x)<1-a,
故选:B
点评:本题主要考查函数零点的应用,根据函数和方程之间的关系,利用数形结合确定a的取值范围是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程sinx=lg|x|实根的个数为( )
| A、6 | B、5 | C、4 | D、3 |
设f(x)=|x-1|(x+1)-x,若关于x的方程f(x)=k有三个不同的实数解,则实数k的取值范围是( )
A、1<k<
| ||
B、-1<k<
| ||
| C、0<k<1 | ||
| D、-1<k<1 |
在区间[-2,3]上随机地取一个数a,则函数f(x)=
x3-ax2+(a+2)x有极值的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线x+y=a与圆x2+y2=9交于两点A、B,且|
+
|=|
-
|,其中O为坐标原点,则实数a的值为( )
| OA |
| OB |
| OA |
| OB |
| A、3 | ||||
| B、-3 | ||||
| C、±3 | ||||
D、±
|
定义域为R的函数y=f(x)的值域为[a,b],则函数y=f(x-3a)的值域为( )
| A、[2a,a+b] |
| B、[0,b-a] |
| C、[a,b] |
| D、[-a,a+b] |
 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a,b满足f(2a+b)<1,则| b+1 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(0,
| ||||
D、(
|
已知P是平面区域
内的动点,向量
=(1,3),则
•
的最小值为( )
|
| a |
| OP |
| a |
| A、-1 | B、-12 |
| C、-6 | D、-18 |