设D.E.F分别△ABC的三边AB.BC.CA的中点.则$\overrightarrow{EA}+\overrightarrow{DC}$=( )A．$\overrightarrow{BC}$B．$3\overrightarrow{DF}$C．$\overrightarrow{BF}$D．$\frac{3}{2}\overrightarrow{BF}$ 题目和参考答案——青夏教育精英家教网——

题目内容

7．设D，E，F分别△ABC的三边AB，BC，CA的中点，则$\overrightarrow{EA}+\overrightarrow{DC}$=（　　）

A．

$\overrightarrow{BC}$

B．

$3\overrightarrow{DF}$

C．

$\overrightarrow{BF}$

D．

$\frac{3}{2}\overrightarrow{BF}$

分析利用向量平行四边形法则即可得出．

解答解：∵$\overrightarrow{AE}$=$\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$，$\overrightarrow{CD}=\frac{1}{2}（\overrightarrow{CA}+\overrightarrow{CB}）$，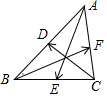
∴$\overrightarrow{EA}+\overrightarrow{DC}$=$-\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$-$\frac{1}{2}（\overrightarrow{CA}+\overrightarrow{CB}）$=$\frac{1}{2}$$（\overrightarrow{BC}+\overrightarrow{BA}）$=$\overrightarrow{BF}$．
故选：C．

点评本题考查了向量平行四边形法则，考查了推理能力与计算能力，属于基础题．

练习册系列答案

每日10分钟口算心算速算天天练系列答案

每时每刻快乐优加系列答案

孟建平培优一号系列答案

孟建平毕业总复习系列答案

密解1对1系列答案

名师导练系列答案

名师讲堂单元同步学练测系列答案

名师面对面中考满分特训方案系列答案

名师名卷单元月考期中期末系列答案

初中总复习教学指南系列答案

相关题目

18．在等差数列{a_n}中，S_n为其前n项和，若a₃+a₄+a₈=25，则S₉=（　　）

19．在极坐标系下，点P是曲线ρ=2（0＜θ＜π）上的动点，A（2，0），线段AP的中点为Q，以极点为原点，极轴为x轴正半轴建立平面直角坐标系．
（1）求点Q的轨迹C的直角坐标方程；
（2）若轨迹C上的点M处的切线斜率的取值范围是[-$\sqrt{3}$，-$\frac{\sqrt{3}}{3}$]，求点M横坐标的取值范围．

15．已知椭圆M：$\frac{x^2}{a^2}+\frac{y^2}{3}$=1（a＞0）的一个焦点为F（-1，0），左、右顶点分别为A，B．经过点F的直线l与椭圆M交于C，D两点．
（1）当直线l的倾斜角为45^°时，求线段CD的长；
（2）记△ABD与△ABC的面积分别为S₁和S₂，求|S₁-S₂|的最大值．

2．已知圆（x+1）²+y²=2，则其圆心和半径分别为（　　）

（1，0），2

（-1，0），2

（1，0），$\sqrt{2}$

（-1，0），$\sqrt{2}$

12．若2是函数f（x）=x³-ax（a∈R）的零点，则在（0，a）内任取一点x₀，使lnx₀＜0的概率是$\frac{1}{4}$．

19．已知正三棱锥的底面边长为2，高为1．
（1）求该正三棱锥的体积；
（2求该正三棱锥的表面积．

16．已知函数y=f（x=2）是偶函数，且当x≠2时其导函数f′（x）满足（x-2）f′（x）＞0，若2＜a＜3，则下列不等式式成立的是（　　）

f（2^a）＜f（3）＜f（log₂^a）

f（3）＜f（log₂^a）＜f（2^a）

f（log₂^a）＜f（3）＜f（2^a）

f（log₂^a）＜f（2^a）＜f（3）

17．已知全集U=R，集M={x|x-3≥0}，N={x|-1≤x＜4}．
（1）求集合M∩N，M∪N；
（2）求集合∁_UN，（∁_UN）∩M．