题目内容
如图,F1、F2是离心率为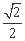 的椭圆C:
的椭圆C: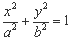 (a>b>0)的左、右
(a>b>0)的左、右
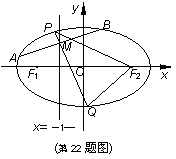
焦点,直线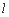 :x=-1将线段F1F2分成两段,其长度之比为1 : 3.设A、B是椭圆C上的两个动点,线段AB的中垂线与椭圆C交于P、Q两点,线段AB的中点M在直线l上.
:x=-1将线段F1F2分成两段,其长度之比为1 : 3.设A、B是椭圆C上的两个动点,线段AB的中垂线与椭圆C交于P、Q两点,线段AB的中点M在直线l上.
(I)求椭圆C的方程;
 (II)求
(II)求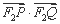 的取值范围.
的取值范围.
 |
 (Ⅰ) 设F2(c,0),则
(Ⅰ) 设F2(c,0),则
 =
= ,
,
所以
c=2.
因为离心率e= , 所以a=
, 所以a= .
.
所以椭圆C的方程为
 . ………… 6分
. ………… 6分
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-1,此时P( ,0)、Q(
,0)、Q( ,0)
,0)
 .
.
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-1,m) (m≠0),A(x1,y1),B(x2,y2).
由  得 (x1+x2)+2(y1+y2)
得 (x1+x2)+2(y1+y2) =0,
=0,
则 -1+2mk=0, 故k= . ………… 8分
. ………… 8分
此时,直线PQ斜率为 ,PQ的直线方程为
,PQ的直线方程为
 . 即
. 即  .
.
联立 消去y,整理得
消去y,整理得
 .
.
所以  ,
, .………… 10分
.………… 10分


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
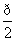 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径. 的不等式
的不等式 和
和 的解集分别为
的解集分别为 和(
和( ),那么称这两个不等式为对偶不等式。如果不等式
),那么称这两个不等式为对偶不等式。如果不等式 与不等式
与不等式 为对偶不等式,且
为对偶不等式,且 ,则
,则 =________________
=________________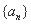 ,如果
,如果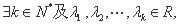
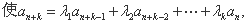 成立,
成立,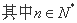 ,则称
,则称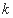 阶递归数列.给出下列三个结论:
阶递归数列.给出下列三个结论:  的整数解恰好有两个,求
的整数解恰好有两个,求 的取值范围是 .
的取值范围是 . 中,若
中,若 ,则
,则 =( )
=( ) 中,
中, ,则
,则 =( )
=( )  B.
B. C.
C. D.
D.

 到
到 ”左端需增加的代数式为( )
”左端需增加的代数式为( ) B.
B.  C.
C.  -
-