题目内容
设θ∈(| π | 2 |
分析:直线的斜率就是直线倾斜角的正切值,然后根据θ∈(
,π)求出倾斜角.
| π |
| 2 |
解答:解:直线xcosθ+ysinθ-1=0的斜率为-cotθ,直线的倾斜角为α,
所以tanα=-cotθ=-tan(
-θ)=tan(θ -
)
因为θ∈(
,π),所以α=θ -
故答案为:θ -
所以tanα=-cotθ=-tan(
| π |
| 2 |
| π |
| 2 |
因为θ∈(
| π |
| 2 |
| π |
| 2 |
故答案为:θ -
| π |
| 2 |
点评:本题考查直线的斜率,直线的倾斜角,考查诱导公式和计算能力,是基础题.

练习册系列答案
相关题目
已知随机变量ξ的分布列为且设η=2ξ+1,则η的期望值是( )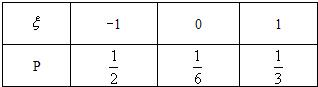

| A、1 | ||
B、
| ||
C、
| ||
D、-
|
已知ξ的分布列如图所示设η=2ξ+1,则Eη=
| ξ | 1 | 2 | 3 | ||||
P |
|
|
b |