题目内容
正方体ABCD-A1B1C1D1，E，F分别是AA1，AB的中点，O是B1D1的中点，则EF，OB所成的角是（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：计算题,空间位置关系与距离,空间角
分析：连接A1B，A1O，运用中位线定理，即可得∠OBA1或补角即为异面直线EF，OB所成的角，设正方体的边长为2，求出三角形OBA1的三边，即可得到所求的角．
解答：
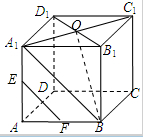解：连接A1B，A1O，
由于E，F分别是AA1，AB的中点，
则EF∥A1B，
即有∠OBA1或补角即为异面直线EF，OB所成的角，
设正方体的边长为2，则A1B=2
，A1O=
，
在直角三角形BB1O中，则有BO=
=
=
，
则有A1O2+BO2=A1B2，即有∠BOA1=90°，
sin∠OBA1=
=
，
则∠OBA1=30°．
故选A．
解：连接A1B，A1O，由于E，F分别是AA1，AB的中点，
则EF∥A1B，
即有∠OBA1或补角即为异面直线EF，OB所成的角，
设正方体的边长为2，则A1B=2
| 2 |
| 2 |
在直角三角形BB1O中，则有BO=
| BB12+B1O2 |
| 4+2 |
| 6 |
则有A1O2+BO2=A1B2，即有∠BOA1=90°，
sin∠OBA1=
| ||
2
|
| 1 |
| 2 |
则∠OBA1=30°．
故选A．
点评：本题考查异面直线所成的角的求法，考查定义法求角的方法，考查运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列函数在x∈（0，+∞）上是增函数的是（ ）
| A、y=x2-2x+3 | ||
| B、y=2-x | ||
C、y=x+
| ||
| D、y=lnx |