题目内容
已知椭圆 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点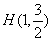 在椭圆上。
在椭圆上。
(1)求椭圆方程;
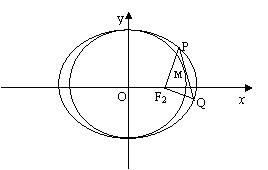
(2)点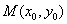 在圆
在圆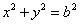 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆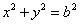 的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由。
的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由。
解:(1) 右焦点为
右焦点为 ,
,

左焦点为 ,点
,点 在椭圆上
在椭圆上

 ,
,
所以椭圆方程为 ----------------5分
----------------5分
(2)设 ,
,

 ------------------------8分
------------------------8分
连接OM,OP,由相切条件知:
 ----------------------------------11分
----------------------------------11分
同理可求
所以 为定值。-------------13分
为定值。-------------13分

练习册系列答案
相关题目
 被两平行线
被两平行线 所截得的线段的长为
所截得的线段的长为 ,则直线
,则直线 ; ②
; ②  ; ③
; ③ 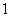 ; ④
; ④  ; ⑤
; ⑤ 
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为 .
的最小值为 .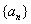 中,对任意正整数
中,对任意正整数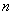 ,都有
,都有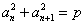 (常数),则称数列
(常数),则称数列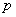 为“公方和”,若数列
为“公方和”,若数列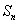 ,且“公方和”为
,且“公方和”为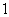 ,首项
,首项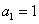 ,则
,则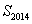 的最大值与最小值之和为( )
的最大值与最小值之和为( )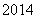 B、
B、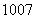 C、
C、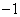 D、
D、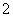
 分别是双曲线
分别是双曲线 的左右焦点,
的左右焦点,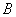 是虚轴的端点,直线
是虚轴的端点,直线 与双曲线
与双曲线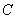 的两条渐近线分别交于
的两条渐近线分别交于 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与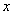 轴交于点
轴交于点 ,若
,若 ,则双曲线
,则双曲线 ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.
 ,且
,且 为第一象限角,则
为第一象限角,则 .
. 为正四面体,
为正四面体, 于点
于点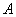 ,点
,点 均在平面
均在平面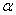 外,且在平面
外,且在平面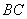 的中点为
的中点为 ,则直线
,则直线 与平面
与平面 B.
B. C.
C. D.
D.

 的定义域为A,值域为B,则
的定义域为A,值域为B,则 =
= B.
B. C.
C. D.
D.