题目内容
如图, 为正四面体,
为正四面体, 于点
于点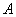 ,点
,点
 均在平面
均在平面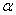 外,且在平面
外,且在平面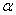 的同一侧,线段
的同一侧,线段
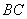 的中点为
的中点为 ,则直线
,则直线 与平面
与平面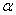 所成角的正弦值为
所成角的正弦值为
A. B.
B. C.
C. D.
D.

A

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图, 为正四面体,
为正四面体, 于点
于点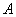 ,点
,点
 均在平面
均在平面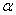 外,且在平面
外,且在平面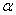 的同一侧,线段
的同一侧,线段
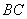 的中点为
的中点为 ,则直线
,则直线 与平面
与平面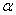 所成角的正弦值为
所成角的正弦值为
A. B.
B. C.
C. D.
D.

A

 名校课堂系列答案
名校课堂系列答案