题目内容
求证: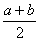
＞2.
解析：考虑分子、分母的关系,可知x2+5=(x2+4)+1,所以用基本公式≥
(a＞0,b＞0)即可得证.
证明：∵x∈R,∴x2≥0.
∴x2+5＞0,x2+4＞0.
∴
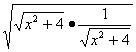≥2·
=2.
∵
时有x2+3=0,这不可能,
∴上述均值不等式中等号不成立.故
＞2.
练习册系列答案
相关题目
＞2.题目内容
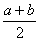求证:＞2.
解析：考虑分子、分母的关系,可知x2+5=(x2+4)+1,所以用基本公式≥(a＞0,b＞0)即可得证.
证明：∵x∈R,∴x2≥0.
∴x2+5＞0,x2+4＞0.
∴
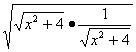≥2·=2.
∵时有x2+3=0,这不可能,
∴上述均值不等式中等号不成立.故＞2.
如图，平面上定点F到定直线l的距离|FM|=2，P为该平面上的动点，过P作直线l的垂线，垂足为Q，且
（2011•唐山一模）如图，直三棱柱ABC-A1B1C1中，AC=BC=1，AAi=3，∠ACB=90°，D为CCi上的点，二面角A-A1B-D的余弦值为-
某校同学设计一个如图所示的“蝴蝶形图案（阴影区域）”，其中AC、BD是过抛物线Γ焦点F的两条弦，且其焦点F（0，1），