题目内容
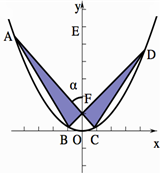 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),| AC |
| BD |
(1)求抛物线Γ方程;
(2)求证:|AF|=
| 2(cosα+1) |
| sin2α |
分析:(1)设出抛物线Γ的标准方程,由焦点坐标算出焦参数p=2,可得抛物线Γ的方程;
(2)过点A作AK⊥y轴于点K,设|AF|=m,在Rt△AFK中利用三角函数的定义算出|AK|=msinα且|FK|=mcosα,可得点A的坐标为(-msinα,1+mcosα),代入抛物线Γ的方程得到关于m、α的等式,将其看作是关于m的一元二次方程,利用求根公式加以计算可得m=
,即|AF|=
成立.
(2)过点A作AK⊥y轴于点K,设|AF|=m,在Rt△AFK中利用三角函数的定义算出|AK|=msinα且|FK|=mcosα,可得点A的坐标为(-msinα,1+mcosα),代入抛物线Γ的方程得到关于m、α的等式,将其看作是关于m的一元二次方程,利用求根公式加以计算可得m=
| 2(cosα+1) |
| sin2α |
| 2(cosα+1) |
| sin2α |
解答:解:(1)设抛物线Γ的方程为x2=2py(P>0),
∵抛物线Γ焦点为F(0,1),∴
=1,解得p=2,
因此,抛物线Γ的方程为x2=4y;
(2)过点A作AK⊥y轴于点K,设|AF|=m,
则Rt△AFK中,∠KFA=α,可得sinα=
,cosα=
,
可得|AK|=|AF|sinα=msinα,|FK|=|AF|cosα=mcosα,
由此可得点A的坐标为(-msinα,1+mcosα)
∵点A为抛物线x2=4y上的点,∴(-msinα)2=4(1+mcosα),
整理得m2sin2α-4mcosα-4=0.将其看作是关于m的一元二次方程,
解得m=
=
=
.
∵α为锐角,可得cosα<1,且m>0.
∴m=
<0不符合题意,得m=
=
即:|AF|=
成立.

∵抛物线Γ焦点为F(0,1),∴
| p |
| 2 |
因此,抛物线Γ的方程为x2=4y;
(2)过点A作AK⊥y轴于点K,设|AF|=m,
则Rt△AFK中,∠KFA=α,可得sinα=
| |AK| |
| |AF| |
| |FK| |
| |AF| |
可得|AK|=|AF|sinα=msinα,|FK|=|AF|cosα=mcosα,
由此可得点A的坐标为(-msinα,1+mcosα)
∵点A为抛物线x2=4y上的点,∴(-msinα)2=4(1+mcosα),
整理得m2sin2α-4mcosα-4=0.将其看作是关于m的一元二次方程,
解得m=
4cosα±
| ||
| 2sin2α |
| 4cosα±4 |
| 2sin2α |
| 2cosα±2 |
| sin2α |
∵α为锐角,可得cosα<1,且m>0.
∴m=
| 2cosα-2 |
| sin2α |
| 2cosα+2 |
| sin2α |
| 2(cosα+1) |
| sin2α |
即:|AF|=
| 2(cosα+1) |
| sin2α |
点评:本题已知抛物线的焦点坐标,求抛物线的方程并证明关于线段AF长的一个等式.着重考查了抛物线的标准方程、直角三角形中三角函数的定义与一元二次方程根的求法等知识,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 、
、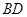 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点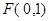 ,
,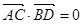 ,点
,点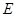 为
为 轴上一点,记
轴上一点,记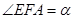 ,其中
,其中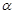 为锐角.
为锐角.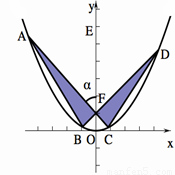
 、
、 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点 ,
, ,点
,点 为
为 轴上一点,记
轴上一点,记 ,其中
,其中 为锐角.
为锐角.
 .
.