题目内容
在平面直角坐标系xoy中，点A（-1，2）、B（2，3）、D（-2，-1）．
（1）求平行四边形ABCD的两条对角线的长；
（2）设向量
-t
与向量
的夹角为锐角，求实数t的取值范围．
（1）求平行四边形ABCD的两条对角线的长；
（2）设向量
| AB |
| OD |
| AD |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由题意易得
和
的坐标，由模长公式可得；
（2）由夹角为锐角可得（
-t
）•
＞0，解t的范围去掉同向的情形即可．
| AC |
| BD |
（2）由夹角为锐角可得（
| AB |
| OD |
| AD |
解答：
解：（1）由题意可得
=（3，5），
=（-1，1），
∴
=
+
=（2，6），∴|
|=
=2
，
同理可得
=
-
=（-4，-4），∴|
|=4
，
∴平行四边形ABCD的两条对角线的长分别为2
，4
；
（2）由（1）可得
-t
=（3+2t，5+t），
由向量
-t
与向量
的夹角为锐角可得（
-t
）•
＞0，
∴-（3+2t）+（5+t）＞0，解得t＜2，
又当t=-
时，两向量同向，夹角为0，不是锐角，
∴实数t的取值范围为t＜2且t≠-
| AB |
| AD |
∴
| AC |
| AB |
| AD |
| AC |
| 22+62 |
| 10 |
同理可得
| BD |
| AD |
| AB |
| BD |
| 2 |
∴平行四边形ABCD的两条对角线的长分别为2
| 10 |
| 2 |
（2）由（1）可得
| AB |
| OD |
由向量
| AB |
| OD |
| AD |
| AB |
| OD |
| AD |
∴-（3+2t）+（5+t）＞0，解得t＜2，
又当t=-
| 8 |
| 3 |
∴实数t的取值范围为t＜2且t≠-
| 8 |
| 3 |
点评：本题考查平面向量数量积的运算，涉及向量夹角为锐角问题，去除同向的情形是解决问题的关键，属基础题．
练习册系列答案
相关题目
向量
=（1，x），
=（-2，1），若
⊥
，则|
|=（ ）
| a |
| b |
| a |
| b |
| a |
A、
| ||
| B、5 | ||
| C、3 | ||
| D、2 |
过点P（0，1）的直线l交抛物线y=x2于A，B两点，点Q为线段AB的中点．若Q点的横坐标为1，则Q点到抛物线焦点的距离为（ ）
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
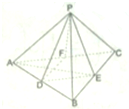如图，在所有棱长都相等的正三棱锥P-ABC中，D，E，F分别是AB，BC，CA的中点，下列四个结论不成立的是（ ）| A、BC∥平面PDF |
| B、平面PDF⊥平面ABC |
| C、平面PAE⊥平面ABC |
| D、平面PDF⊥平面PAE |
如图是某几何体的三视图，则该几何体的外接球的体积为（ ）
| A、8π | ||||
B、
| ||||
C、
| ||||
| D、64π |