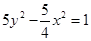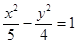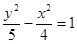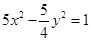题目内容
若抛物线y2=ax上恒有关于直线x+y-1=0对称的两点A,B,则a的取值范围是( )
A. |
B. |
C. |
D. |
C
解析试题分析:设A(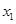 ,
,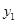 ),B(
),B(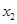 ,
,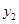 ),
),
因为点A和B在抛物线上,所以有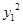 =a
=a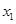 ①
①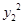 =a
=a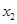 ②
②
①-②得,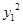 ?
? 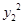 =a(
=a(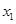 ?
? 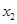 ).
).
整理得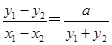 ,
,
因为A,B关于直线x+y-1=0对称,所以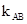 =1,即
=1,即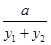 =1.
=1.
所以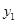 +
+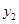 =a.
=a.
设AB的中点为M(x0,y0),则y0=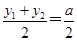 .
.
又M在直线x+y-1=0上,所以x0=1?y0=1? 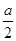 .
.
则M(1?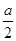 ,
,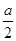 ).
).
因为M在抛物线内部,所以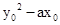 <0.
<0.
即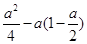 <0,解得0<a<
<0,解得0<a<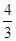 .故选C.
.故选C.
考点:直线与抛物线的位置关系
点评:中档题,“点差法”是解决与弦中点有关问题的常用方法,解答的关键是由AB中点在抛物线内部得到关于a的不等式.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
抛物线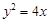 的焦点为
的焦点为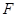 ,点
,点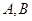 在抛物线上,且
在抛物线上,且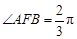 ,弦
,弦 中点
中点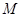 在准线
在准线 上的射影为
上的射影为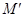 ,则
,则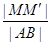 的最大值为( )
的最大值为( )
A.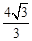 | B.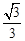 | C.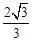 | D.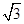 |
已知双曲线
 以及双曲线
以及双曲线
 的渐近线将第一象限三等分,则双曲线
的渐近线将第一象限三等分,则双曲线 的离心率为( )
的离心率为( )
A.2或 | B. 或 或 | C.2或 | D. 或 或 |
已知椭圆 的长轴在
的长轴在 轴上,且焦距为4,则
轴上,且焦距为4,则 等于( )
等于( )
| A.4 | B.5 | C.7 | D.8 |
已知双曲线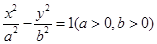 ,两渐近线的夹角为
,两渐近线的夹角为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.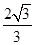 | B.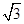 | C. | D.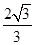 或 或 |
抛物线 上的一动点
上的一动点 到直线
到直线 距离的最小值是 ( )
距离的最小值是 ( )
A. | B. | C. | D. |
 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若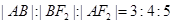 ,则双曲线的离心率是( )
,则双曲线的离心率是( )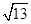
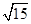
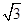
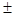 4y=0,则 该双曲线的标准方程为( )
4y=0,则 该双曲线的标准方程为( )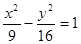
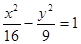
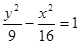

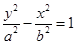 的一个焦点与抛物线
的一个焦点与抛物线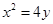 的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )