题目内容
抛物线 上的一动点
上的一动点 到直线
到直线 距离的最小值是 ( )
距离的最小值是 ( )
A. | B. | C. | D. |
A
解析试题分析:对y=x2求导可求与直线x-y-1=0平行且与抛物线y=x2相切的切线方程,然后利用两平行线的距离公司可得所求的最小距离d。解:(法一)对y=x2求导可得y′=2x,令y′=2x=1可得x= ∴与直线x-y-1=0平行且与抛物线y=x2相切的切点(
∴与直线x-y-1=0平行且与抛物线y=x2相切的切点( ,
, ),切线方程为y-
),切线方程为y- =x-
=x- 即x-y-
即x-y- =0由两平行线的距离公司可得所求的最小距离d=
=0由两平行线的距离公司可得所求的最小距离d=
 ,故选A.
,故选A.
考点:直线与抛物线的位置关系
点评:本题考查直线与抛物线的位置关系的应用,解题时要注意公式的灵活运用,抛物线的基本性质和点到线的距离公式的应用,考查综合运用能力

练习册系列答案
相关题目
已知三个数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为
的离心率为
A. | B. | C. 或 或 | D. 或 或 |
知圆柱的底面半径为2,高为3,用一个平面去截,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )
A. | B.(0, | C. | D.(0,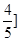 |
双曲线 的渐近线方程为( )
的渐近线方程为( )
A. | B. | C. | D. |
设抛物线C:y2=4x的焦点为F,直线 过F且与C交于A, B两点.若|AF|=3|BF|,则
过F且与C交于A, B两点.若|AF|=3|BF|,则 的方程为( )
的方程为( )
| A.y=x-1或y=-x+1 |
B.y=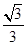 (X-1)或y= (X-1)或y= (x-1) (x-1) |
C.y=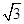 (x-1)或y= (x-1)或y= (x-1) (x-1) |
D.y= (x-1)或y= (x-1)或y=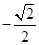 (x-1) (x-1) |
双曲线 的离心率大于
的离心率大于 的充分必要条件是( )
的充分必要条件是( )
A. | B.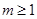 | C. | D. |




 的左、右焦点,P为直线
的左、右焦点,P为直线 上一点,
上一点,



 ,则双曲线的的离心率为( )
,则双曲线的的离心率为( )
