题目内容
设数列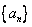 的首项
的首项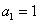 ,前
,前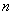 项和为
项和为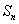 ,且点
,且点 在直线
在直线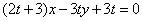 (
(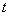 为与
为与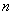 无关的正实数)上,
无关的正实数)上,
(1)求证:数列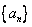 是等比数列;
是等比数列;
(2)记数列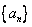 的公比为
的公比为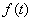 ,数列
,数列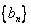 满足
满足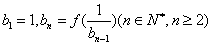 ,设
,设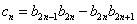 ,求数列
,求数列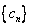 的前
的前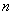 项和
项和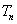 ;
;
(3)在(2)的条件下,设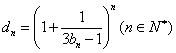 ,证明:
,证明: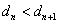 .
.
【答案】
(1)因为点 在直线
在直线 (
( 为与
为与 无关的正实数)上,所以
无关的正实数)上,所以 ,即有
,即有 .
.
当 时,
时, .
.
由 ,解得
,解得 ,所以
,所以 .
.
当 时,有
时,有
 ……………………………………………………①
……………………………………………………①
 ……………………………………………………②
……………………………………………………②
①-②,得 ,整理得
,整理得 .
.


 .……………………………………8分
.……………………………………8分
(3)由(2)知 ,则
,则
将 用二项式定理展开,共有
用二项式定理展开,共有 项,其第
项,其第 项为
项为 为
为
 ,
,
同理, 用二项式定理展开,共有
用二项式定理展开,共有 项,第
项,第 项为
项为 ,其前
,其前 项中的第
项中的第 项
项 为
为
 ,
,
由 ,
, ,…,
,…, ,
,
得 ,
, ,又T1 = U1,T2 = U2,
,又T1 = U1,T2 = U2, ,
,
∴ .……………………………………………………14分
.……………………………………………………14分

练习册系列答案
相关题目
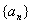 的首项
的首项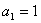 ,前
,前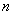 项和为
项和为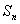 (
(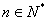 ),且点
),且点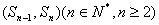 在直线
在直线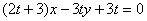 上(
上(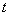 为与
为与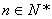 )为等比数列;
)为等比数列;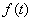 ,数列
,数列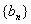 满足
满足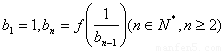 ,设
,设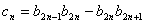 ,求数列
,求数列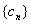 的前
的前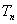 ;
;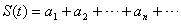 ,求函数
,求函数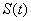 的值域.
的值域.