题目内容
设数列{![]() }的首项
}的首项![]() ,前
,前![]() 项和S
项和S![]() 满足关系式
满足关系式![]() (其中
(其中![]() =1,2,3,4,…).
=1,2,3,4,…).
(Ⅰ)求证:数列{![]() }是等比数列;
}是等比数列;
(Ⅱ)设数列{![]() }的公比为
}的公比为![]() ,作数列{
,作数列{![]() },使
},使![]() ,(
,(![]() =2,3,4,…),求数列{
=2,3,4,…),求数列{![]() }的通项公式;
}的通项公式;
(Ⅲ)求和:![]() .
.
解:(Ⅰ)![]() ,当
,当![]() 时,由
时,由
得![]() .
.
∴![]() ,
,
∴![]()
故{![]() }为等比数列,首项为1,公比为
}为等比数列,首项为1,公比为![]() .
.
(Ⅲ)∵![]() ,
,
![]() ,
,
∴![]() 是以1为首项,
是以1为首项,![]() 为公差的等差数列,故其通项公式为
为公差的等差数列,故其通项公式为
![]() .
.
(Ⅲ)(解法一)∵![]() ,
,![]() ,
,![]()
∴{![]() },{
},{![]() }是首项分别为
}是首项分别为![]() 和1,公差均为
和1,公差均为![]() 的等差数列.
的等差数列.
①当![]() …)时,
…)时,
![]() ,
,
=![]()
=![]() (*)
(*)
=![]()
=![]() .
.
②当![]() …)时,
…)时,
![]()
=![]()
=![]()
=![]() (由(*))
(由(*))
=![]() .
.
综上,
(解法二)∵![]()
=![]() .
.
∴当![]() 为偶数时
为偶数时
![]()
=
=![]() ;
;
当![]() 为奇数时
为奇数时
![]()
=![]()
=
=![]()
综上,

练习册系列答案
相关题目
 ,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).
,前n项和为Sn,且满足2an+1+Sn=3( n∈N*). 的所有n的值.
的所有n的值.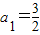 ,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).
,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).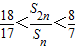 的所有n的值.
的所有n的值.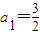 ,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).
,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).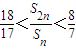 的所有n的值.
的所有n的值.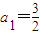 ,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).
,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).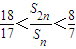 的所有n的值.
的所有n的值. ,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).
,前n项和为Sn,且满足2an+1+Sn=3( n∈N*).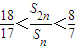 的所有n的值.
的所有n的值.