题目内容
设无穷数列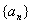 的首项
的首项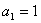 ,前
,前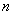 项和为
项和为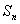 (
(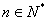 ),且点
),且点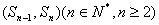 在直线
在直线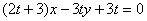 上(
上(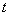 为与
为与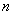 无关的正实数).
无关的正实数).
(1)求证:数列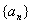 (
(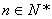 )为等比数列;
)为等比数列;
(2)记数列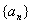 的公比为
的公比为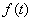 ,数列
,数列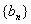 满足
满足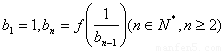 ,设
,设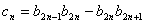 ,求数列
,求数列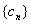 的前
的前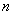 项和
项和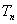 ;
;
(3)(理)若(1)中无穷等比数列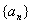 (
(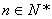 )的各项和存在,记
)的各项和存在,记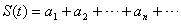 ,求函数
,求函数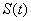 的值域.
的值域.
【答案】
(1)证明见解析;(2)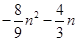 ;(3)
;(3)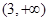 .
.
【解析】
试题分析:(1)把已知条件变形为 ,要化为数列项的关系,一般方法是用
,要化为数列项的关系,一般方法是用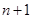 代
代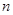 得
得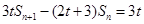 ,两式相减,得
,两式相减,得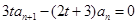 ,从而得前后项比
,从而得前后项比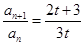 为常数,只是还要注意看看是不是有
为常数,只是还要注意看看是不是有 ,如有则可证得
,如有则可证得 为等比数列;(2)由
为等比数列;(2)由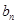 定义可知数列
定义可知数列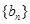 是等差数列,
是等差数列,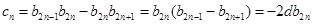 (
(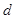 是数列
是数列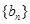 公差),从而数列
公差),从而数列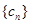 也是等差数列,其前
也是等差数列,其前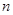 和易得,这说明我们在求数列和时,最好能确定这个数列是什么数列;(3)首先无穷等比数列
和易得,这说明我们在求数列和时,最好能确定这个数列是什么数列;(3)首先无穷等比数列 的和存在说明公比
的和存在说明公比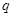 满足
满足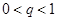 ,从而得出
,从而得出 ,无穷等比数列的和公式得
,无穷等比数列的和公式得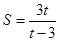 ,这是一次分式函数,其值域采用分离分式法,即
,这是一次分式函数,其值域采用分离分式法,即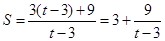 ,易得
,易得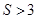 .
.
试题解析:(1)由已知,有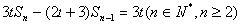 ,
,
当 时,
时,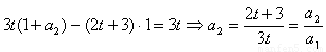 ; 2分
; 2分
当 时,有
时,有 ,
,
两式相减,得 ,即
,即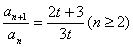 ,
,
综上, ,故数列
,故数列 是公比为
是公比为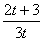 的等比数列; 4分
的等比数列; 4分
(2)由(1)知,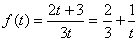 ,则
,则
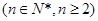
于是数列 是公差
是公差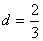 的等差数列,即
的等差数列,即 ,
7分
,
7分
则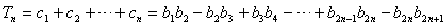

= 10分
10分
(3)(理)由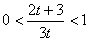 解得:
解得: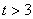 。
12分
。
12分
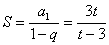 14分
14分
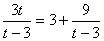 ,当
,当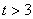 时,
时, ,函数
,函数 的值域为
的值域为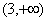 。 16分
。 16分
考点:(1)数列的前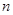 项和
项和 与
与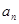 的关系,等比数列的定义;(2)等差数列的前
的关系,等比数列的定义;(2)等差数列的前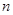 项和;(3)无穷等比数列的和及一次分式函数的值域.
项和;(3)无穷等比数列的和及一次分式函数的值域.

练习册系列答案
相关题目
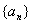 的首项
的首项 ,前
,前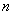 项和为
项和为 (
( ),且点
),且点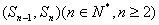 在直线
在直线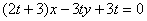 上(
上(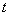 为与
为与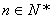 )为等比数列;
)为等比数列;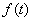 ,数列
,数列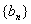 满足
满足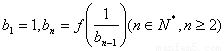 ,设
,设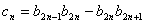 ,求数列
,求数列 的前
的前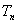 ;
; 时不等式
时不等式 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。