题目内容
求过A(1,4)，B(3,2)两点，且圆心在直线y＝0上的圆的标准方程，并判断点M1(2,3)，M2(2,4)与圆的位置关系．
解析：根据圆的标准方程，只要求得圆心坐标和圆的半径即可．
因为圆过A，B两点，所以圆心在线段AB的垂直平分线上．由kAB＝
＝－1，AB的中点为(2,3)，故AB的垂直平分线的方程为y－3＝x－2，即x－y＋1＝0.
又圆心在直线y＝0上，因此圆心坐标是方程组
的解，即圆心坐标为(－1,0)，半径r＝
＝
，所以得所求圆的标准方程为(x＋1)2＋y2＝20.
因为M1到圆心C(－1,0)的距离为
＝
，|M1C|<r，所以M1在圆C内；而点M2到圆心C的距离|M2C|＝
＝
>，所以M2在圆C外．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
－
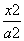＝1(a>0，b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界)，若点(1,2)在“上”区域内，则双曲线离心率e的取值范围是____________．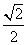
.
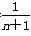(n∈N*)与椭圆C在第一象限内相交于点An(xn，yn)，记an＝
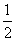x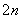
，试证明：对∀n∈N*
，a1·a2·…·an＞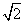
D．5
原点的对称点是( )
|
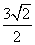.设P为直线l上的点，过点P作抛物线C的两条切线PA，PB，其中A，B为切点．