Question

（2011•深圳二模）如图1，在直角梯形ABCD中，AB∥CD，AB⊥AD，且AB=AD=

1

2

CD=1．现以AD为一边向形外作正方形ADEF，然后沿边AD将正方形ADEF翻折，使平面ADEF与平面ABCD互相垂直，如图2．

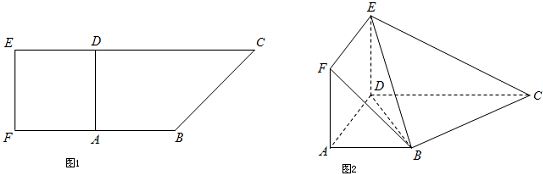
（1）求证：平面BDE⊥平面BEC；
（2）求平面ABCD与平面EFB所成锐二面角的大小．

Answer 1

分析：（1）证明平面BDE⊥平面BEC，只需证明BC⊥平面BDE，根据直线与平面垂直的判定定理可知只需证BC与平面BDE内两相交直线垂直，根据面面垂直的性质可知ED⊥平面ABCD，则ED⊥BC，根据勾股定理可知BC⊥BD，满足定理所需条件；
（2）过E作EG⊥BC，连接DG，则∠EGD为平面ABCD与平面EFB所成角，利用三角函数可得结论．

解答：（1）证明：在正方形ADEF中，ED⊥AD．
又因为平面ADEF⊥平面ABCD，且平面ADEF∩平面ABCD=AD，
所以ED⊥平面ABCD．
所以ED⊥BC．
在直角梯形ABCD中，AB=AD=1，CD=2，可得BC=

2

．
在△BCD中，BD=BC=

2

，
所以BD²+BC²=CD²．
所以BC⊥BD．
所以BC⊥平面BDE．
因为BC?平面BEC，所以平面BDE⊥平面BEC；
（2）解：过E作EG⊥BC，连接DG，则
∵AB⊥AD，沿边AD将正方形ADEF翻折，使平面ADEF与平面ABCD互相垂直，
∴ED⊥平面ABCD
∴∠EGD为平面ABCD与平面EFB所成角
∵AB=AD=

1

2

CD=1
∴DG=

2

，ED=1
∴tan∠EGD=

1

2

=

2

2

∴∠EGD=arctan

2

2

．

点评：本题考查的知识点是平面与平面垂直的判定，考查面面角，考查学生分析解决问题的能力，属于中档题．