题目内容
设向量
=（cosα，sinα），
=（cosβ，sinβ），其中0＜β＜α＜π．
（1）若
⊥
，求|
+
|的值；
（2）设向量
=(0，
)，且
+
=
，求α，β的值．
| a |
| b |
（1）若
| a |
| b |
| a |
| 3 |
| b |
（2）设向量
| c |
| 3 |
| a |
| b |
| c |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）利用数量积的运算性质即可得出；
（2）利用向量相等和诱导公式、三角函数的单调性即可得出．
（2）利用向量相等和诱导公式、三角函数的单调性即可得出．
解答：
解：（1）∵
=（cosα，sinα），
=（cosβ，sinβ），
∴|
|=1，|
|=1．
∵
⊥
，∴
•
=0．
于是|
+
|=
=
=2．
故|
+
|=2．
（2）∵
+
=(cosα+cosβ ， sinα+sinβ)=(0 ，
)，
∴
，
由此得cosα=cos（π-β），
由0＜β＜π，得0＜π-β＜π，
又0＜α＜π，故α=π-β．
代入sinα+sinβ=
，得sinα=sinβ=
．
而0＜β＜α＜π，∴α=
， β=
．
| a |
| b |
∴|
| a |
| b |
∵
| a |
| b |
| a |
| b |
于是|
| a |
| 3 |
| b |
|
| 12+3×12 |
故|
| a |
| 3 |
| b |
（2）∵
| a |
| b |
| 3 |
∴
|
由此得cosα=cos（π-β），
由0＜β＜π，得0＜π-β＜π，
又0＜α＜π，故α=π-β．
代入sinα+sinβ=
| 3 |
| ||
| 2 |
而0＜β＜α＜π，∴α=
| 2π |
| 3 |
| π |
| 3 |
点评：本题考查了数量积的运算性质、向量相等和诱导公式、三角函数的单调性等基础知识与基本技能方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
有一个圆形卡片，如图所示，共分4块区域，上下左右对称，现有4种不同颜色可供选择填涂，要求相邻区域不能填涂同种颜色，填涂方法共有（ ）种．| A、24 | B、54 | C、60 | D、108 |
己知函数f（x）=lnx+
，则下列结论中正确的是（ ）
| 1 |
| lnx |
| A、若x1，x2（x1＜x2）是f（x）的极值点，则f（x）在区间（x1，x2）内是增函数 |
| B、若x1，x2（x1＜x2）是f（x）的极值点，则f（x）在区间（x1，x2）内是减函数 |
| C、?x＞0，且x≠1，f（x）≥2 |
| D、?x0＞0，f（x）在（x0，+∞）上是增函数 |
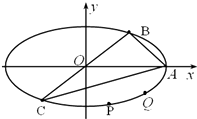如图，椭圆
某音乐喷泉喷射的水珠呈抛物线形，它在每分钟内随时间t（秒）的变化规律大致可用y=-（1+4sin2