题目内容
5．若关于x的二次方程mx2+（2m-1）x-m+2=0（m＞0）的两个互异的实根都小于1，则实数m的取值范围是（$\frac{3+\sqrt{7}}{4}$，+∞）．分析 根据一元二次方程根的分布与系数的关系，二次函数的性质，列出不等式组，解不等式组求得m的范围．
解答 解：∵关于x的二次方程mx2+（2m-1）x-m+2=0（m＞0）的两个互异的实根都小于1，则 $\left\{\begin{array}{l}{m＞0}\\{△{=（2m-1）}^{2}-4m（-m+2）＞0}\\{\frac{1-2m}{m}＜1}\\{f（1）=m+2m-1-m+2＞0}\end{array}\right.$，
即$\left\{\begin{array}{l}{m＞0}\\{m＜\frac{3-\sqrt{7}}{4}，或m＞\frac{3+\sqrt{7}}{4}}\\{m＞\frac{1}{4}}\\{m＞-\frac{1}{2}}\end{array}\right.$ 求得m＞$\frac{3+\sqrt{7}}{4}$，即m的范围为（$\frac{3+\sqrt{7}}{4}$，+∞），
故答案为：（$\frac{3+\sqrt{7}}{4}$，+∞）．
点评 本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，属于基础题．
练习册系列答案
相关题目
16．要得到函数y=sin$\frac{1}{2}$x的图象，只需将函数y=sin（$\frac{1}{2}$x+$\frac{π}{6}$）的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
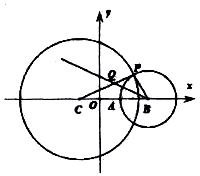如图，在平面直角坐标系xoy中，已知圆C：（x+1）2+y2=16，点A（1，0），点B（a，0）（|a|＞3），以B为圆心，|BA|的半径作圆，交圆C于点P，且的∠PBA的平分线次线段CP于点Q．