题目内容
6.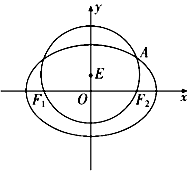 如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.(Ⅰ)求椭圆C的方程;
(Ⅱ)设与直线OA(O为原点)平行的直线l交椭圆C于M,N两点.当△AMN的面积取到最大值时,求直线l的方程.
分析 (I)根据圆的性质求出焦点和A点坐标,利用椭圆的定义得2a=|AF1|-|AF2|,从而得出a,进而得出椭圆的方程;
(II)设直线l的方程为y=$\frac{\sqrt{2}}{2}x$+m,联立方程组消元,利用根与系数的关系求出|MN|,用m表示出△AMN的面积,根据m的范围求出三角形的面积.
解答 解:(Ⅰ)∵F1,E,A三点共线,∴F1A为圆E的直径,且AF1=3,∴AF2⊥F1F2.
由${x^2}+{({0-\frac{1}{2}})^2}=\frac{9}{4}$,得$x=±\sqrt{2}$,∴$c=\sqrt{2}$.
∵${|{A{F_2}}|^2}={|{A{F_1}}|^2}-{|{{F_1}{F_2}}|^2}=9-8=1$,∴AF2=1,
∴2a=|AF1|+|AF2|=4,a=2.
∵a2=b2+c2,∴$b=\sqrt{2}$,
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(Ⅱ)由(Ⅰ)知,点A的坐标为$({\sqrt{2},1})$,∴直线OA的斜率为$\frac{{\sqrt{2}}}{2}$.
设直线l的方程为$y=\frac{{\sqrt{2}}}{2}x+m$,
联立$\left\{\begin{array}{l}y=\frac{{\sqrt{2}}}{2}x+m\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$得,${x^2}+\sqrt{2}mx+{m^2}-2=0$,
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=-\sqrt{2}m$,${x_1}{x_2}={m^2}-2$,
∵△=2m2-4m2+8>0,∴-2<m<2.
又$|{MN}|=\sqrt{1+{k^2}}|{{x_2}-{x_1}}|$=$\sqrt{1+\frac{1}{2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=\sqrt{12-3{m^2}}$,
∵点A到直线l的距离$d=\frac{{\sqrt{6}|m|}}{3}$,
∴${S_{△AMN}}=\frac{1}{2}|{MN}|•d=\frac{1}{2}\sqrt{12-3{m^2}}×\frac{{\sqrt{6}}}{3}|m|$
=$\frac{{\sqrt{2}}}{2}\sqrt{({4-{m^2}})•{m^2}}≤\frac{{\sqrt{2}}}{2}×\frac{{({4-{m^2}})+{m^2}}}{2}=\sqrt{2}$,
当且仅当4-m2=m2,即$m=±\sqrt{2}$时等号成立,
此时直线l的方程为$y=\frac{{\sqrt{2}}}{2}x±\sqrt{2}$.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.

 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
| A. | -5 | B. | 2 | C. | 5 | D. | 7 |
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相离 |