题目内容
16.直线ax-y+$\sqrt{2}$a=0(a≥0)与圆x2+y2=9的位置关系是( )| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相离 |
分析 求出直线恒过的定点,判断定点与圆的位置关系.
解答 解:直线ax-y+$\sqrt{2}$a=0(a≥0),即a(x+$\sqrt{2}$)-y=0,令x+$\sqrt{2}$=0,y=0,可得恒过定点(-$\sqrt{2}$,0),而(-$\sqrt{2}$,0)满足2+02<9,所以直线与圆相交.
故选:A.
点评 本题是基础题,考查直线与圆的位置关系,判断关系的方法是点在圆的内部与外部或圆上是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7.执行如图所示程序框图,若使输出的结果不大于100,则输入的整数k的最大值为( )

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.设△ABC的内角A,B,C分别对应边a,b,c.若c2=(a-b)2+6,${S_{△ABC}}=\frac{3}{2}\sqrt{3}$,则角C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{3}{4}π$ | D. | $\frac{2}{3}π$ |
1.已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),若对任意实数x都有x2f′(x)>2xf(-x),则不等式x2f(x)<(3x-1)2f(1-3x)的解集是( )
| A. | ($\frac{1}{4}$,+∞) | B. | (0,$\frac{1}{4}$) | C. | (-∞,$\frac{1}{4}$) | D. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) |
5.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上一点到两个焦点的距离分别为10和4,且离心率为2,则该双曲线的虚轴长为( )
| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
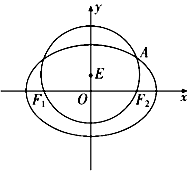 如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.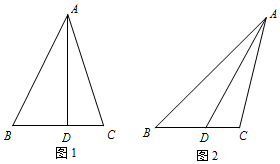 如图,在△ABC中,D为边BC上一点,AD=6,BD=3,
如图,在△ABC中,D为边BC上一点,AD=6,BD=3,