题目内容
9.若复数z满足($\sqrt{3}$+i)•z=4i,其中i为虚数单位,则z=( )| A. | 1-$\sqrt{3}$i | B. | $\sqrt{3}$-i | C. | $\sqrt{3}$+i | D. | 1+$\sqrt{3}$i |
分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:∵($\sqrt{3}$+i)•z=4i,
∴$z=\frac{4i}{\sqrt{3}+i}=\frac{4i(\sqrt{3}-i)}{(\sqrt{3}+i)(\sqrt{3}-i)}=1+\sqrt{3}i$,
故选:D.
点评 本题考查复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
4.已知函数f(x)=Asin(ωx+φ)(A≠0,ω>0,0<φ<$\frac{π}{2}$),若f($\frac{2π}{3}$)=-f(0),则ω的最小值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
16.若双曲线的右顶点与抛物线y2=12x的焦点相同,它们的离心率之和是3,该双曲线的标准方程是( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}=1$ | B. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{10}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{9}$=1 |
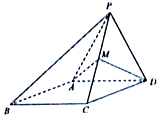 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
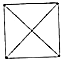
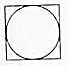
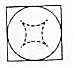
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.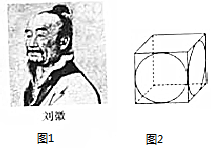 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )