题目内容
设p：函数f（x）=
的定义域为R；q：?m∈[-1，1]，a2-5a-5≥m2恒成立；如果“p∨q”为真命题，且“p∧q”为假命题，求实数a的取值范围．
| x2-4x+a2 |
考点：复合命题的真假
专题：简易逻辑
分析：根据条件求出命题p，q为真命题的等价条件，利用复合命题与简单命题之间的关系即可得到结论．
解答：
解：∵函数f（x）=
的定义域为R，
∴x2-4x+a2≥0恒成立，则判别式△=16-4a2≤0，解得a≥2或a≤-2．
即p：a≥2或a≤-2．
∵?m∈[-1，1]，a2-5a-5≥m2恒成立；
∴a2-5a-5≥1，即a2-5a-6≥0，解得a≥6或a≤-1．即q：a≥6或a≤-1，
∵“p∨q”为真命题，且“p∧q”为假命题，
∴p，q一真，一假，
①若p真，q假，则
，解得2≤a＜6，
②若p假，q真，则
，解得-2＜a≤-1，
综上实数a的取值范围是（-2，-1]∪[2，6）．
| x2-4x+a2 |
∴x2-4x+a2≥0恒成立，则判别式△=16-4a2≤0，解得a≥2或a≤-2．
即p：a≥2或a≤-2．
∵?m∈[-1，1]，a2-5a-5≥m2恒成立；
∴a2-5a-5≥1，即a2-5a-6≥0，解得a≥6或a≤-1．即q：a≥6或a≤-1，
∵“p∨q”为真命题，且“p∧q”为假命题，
∴p，q一真，一假，
①若p真，q假，则
|
②若p假，q真，则
|
综上实数a的取值范围是（-2，-1]∪[2，6）．
点评：本题主要考查复合命题与简单命题之间的关系，求出命题p，q的等价条件是解决本题的关键．
练习册系列答案
相关题目
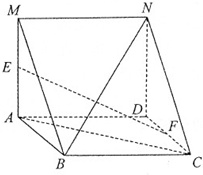如图，四边形ABCD是菱形，四边形MADN是矩形，平面MADN⊥平面ABCD，E，F分别为MA，DC的中点，求证：