题目内容
13.已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC,若点P的坐标为(3,0),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的最小值为2.分析 由题意知AC为直径,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|=|2$\overrightarrow{PO}$+$\overrightarrow{PB}$|,
利用不等式的性质求出|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的最小值.
解答 解:由AB⊥BC知,AC为直径,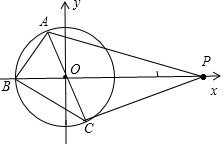
∴|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|=|2$\overrightarrow{PO}$+$\overrightarrow{PB}$|≥|2$\overrightarrow{PO}$|-|$\overrightarrow{PB}$|=6-|$\overrightarrow{PB}$|;
∴当B为(-1,0)时,6-|PB|≥6-4=2,
∴|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|取得最小值为2.
故答案为:2.
点评 本题考查了直线与圆的方程应用问题,也考查了不等式的应用问题,是基础题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
3.若将函数y=8sin2x的图象向左平移φ(φ>0)个单位长度,得到的函数图象关于原点对称,则cos4φ+sin4φ=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
8.将5名大学生分配到A,B,C 3个乡镇去任职,每个乡镇至少一名,那么A镇分得两位大学生的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
18.在区间[1,e]上任取实数a,在区间[0,1]上任取实数b,使函数f(x)=ax2+x+$\frac{1}{4}$b有两个相异零点的概率是( )
| A. | $\frac{1}{e-1}$ | B. | $\frac{1}{2(e-1)}$ | C. | $\frac{1}{4(e-1)}$ | D. | $\frac{1}{8(e-1)}$ |