题目内容
18.函数f(x)=$\frac{ax}{ax+1}$,a≠0,a为常数,方程f(x)=x有唯一实数解(1)求f(x)
(2)x1=2,xn+1=f(xn),n∈N*,求证:数列{$\frac{1}{{x}_{n}}$}为等差数列,并求xn.
分析 (1)方程f(x)=x有唯一解,求出a的值,从而求出函数的表达式,
(2)由题意可知,xn+1=$\frac{{x}_{n}}{{x}_{n}-1}$,继而得到$\frac{1}{{x}_{n+1}}$-$\frac{1}{{x}_{n}}$=1,数列{$\frac{1}{{x}_{n}}$}是以$\frac{1}{2}$为首项,以1为公差的等差数列,即可求出通项公式.
解答 解:(1)f(x)=$\frac{ax}{ax+1}$,a≠0,a为常数,方程f(x)=x,
∴ax2+x=ax,
即ax2+x(1-a)=0,
∴△=(1-a)2=0,
解得a=1,
∴f(x)=$\frac{x}{x+1}$,
(2)xn+1=f(xn),
∴xn+1=$\frac{{x}_{n}}{{x}_{n}-1}$,
∴xn+1xn-xn+1=xn,
∴$\frac{1}{{x}_{n+1}}$-$\frac{1}{{x}_{n}}$=1,
∵x1=2,
∴$\frac{1}{{x}_{1}}$=$\frac{1}{2}$,
∴数列{$\frac{1}{{x}_{n}}$}是以$\frac{1}{2}$为首项,以1为公差的等差数列,
∴$\frac{1}{{x}_{n}}$=$\frac{1}{2}$+(n-1)=n-$\frac{1}{2}$,
∴xn=$\frac{2}{2n-1}$,
当n=1时,成立,
故xn=$\frac{2}{2n-1}$.
点评 本题考查等差数列的证明,考查数列的通项公式,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知函数f(x)=cos(sinx)+sin(cosx).则下列结论正确的是( )
| A. | f(x)的周期为π | B. | f(x)在(-$\frac{π}{2}$,0)上单调递减 | ||
| C. | f(x)的最大值为$\sqrt{2}$ | D. | f(x)的图象关于直线x=π对称 |
6.已知圆x2+y2=17在点(1,4)处的切线与幂函数f(x)的图象在点A(1,f(1))处的切线垂直,且不等式$\frac{f(x)}{x}$>ax2+x在(1,2)上能成立,则实数a的取值范围为( )
| A. | [0,+∞) | B. | ($\frac{35}{6}$,+∞) | C. | (-∞,0] | D. | (-∞,$\frac{3}{2}$) |
13.log3(log82)等于( )
| A. | -1 | B. | 1 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
7.下列表述正确的是( )
| A. | 过平面β外一点可以作无数条直线与平面β平行 | |
| B. | 过直线l外一点可作无数条直线平行于l | |
| C. | 垂直于两条异面直线的空间直线只有一条 | |
| D. | 空间三个平面最多把空间分成七部分 |
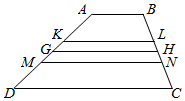 如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.
如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.