题目内容
6.若sin4θ+co4sθ=1,则sinθcosθ的值为0.分析 先利用同角三角函数及二倍角公式对sin4θ+cos4θ化简整理求的sin22θ=0,进而求得sinθcosθ的值.
解答 解:sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1-2sin2θcos2θ=1,
∴2sin2θcos2θ=0,
∴sinθcosθ=0.
故答案为:0.
点评 本题主要考查了同角三角函数基本关系,二倍角公式的应用.考查了学生创造思维和分析问题的能力,属于基础题.

练习册系列答案
相关题目
16.三棱锥P-ABC三条侧棱两两垂直,三条侧棱长分别为1,$\sqrt{5}$,$\sqrt{10}$,则该三棱锥的外接球体积为( )
| A. | $\frac{32}{3}$π | B. | $\frac{16}{3}$π | C. | 32π | D. | 16π |
18.两平行线4x+3y+5=0与4x+3y+15=0之间的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.已知O是平面内任意一点,α是任意角,下列等式一定可以判定A,B,C三点共线的是( )
| A. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$+cosα$\overrightarrow{OB}$ | B. | $\overrightarrow{OC}$=sin2α$\overrightarrow{OA}$+cos2α$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OC}$=sinα$\overrightarrow{OA}$-cosα$\overrightarrow{OB}$ | D. | $\overline{OC}$=sin2α$\overrightarrow{OA}$-cos2α$\overrightarrow{OB}$ |
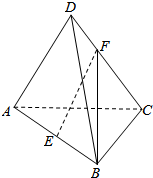 如图,在空间四边形ABCD中,E是线段AB的中点.
如图,在空间四边形ABCD中,E是线段AB的中点.